Ans: B
Join $BC$ and $OC$, where $O$ is the centre of the semicircle.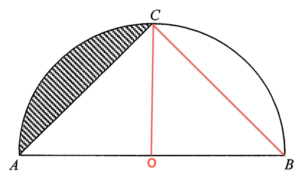
Join $BC$ and $OC$, where $O$ is the centre of the semicircle.

Since $AB$ is the diameter of the semicircle, then $\angle ACB = 90^\circ$. Therefore, we have
$\begin{array}{rcl}
\sin \angle ABC & = & \dfrac{AC}{AB} \\
& = & \dfrac{2}{3} \\
\angle ABC & = & 41.810~314~89^\circ
\end{array}$
Hence, we have
$\begin{array}{rcl}
\angle AOC & = & 2 \times \angle ABC \\
& = & 83.620~629~78^\circ
\end{array}$
Therefore, the area of the shaded region
$\begin{array}{cl}
= & \pi (1.5)^2 \times \dfrac{83.620~629~78^\circ}{360^\circ} – \dfrac{1}{2} (1.5)(1.5) \sin 83.620~629~78^\circ \\
= & 0.523~853~237 \text{ cm}^2 \\
= & 0.52 \text{ cm}^2 \text{, correct to the nearest $0.01$ cm$^2$}
\end{array}$

