Ans: D
Add a rectangle on the figure as shown below.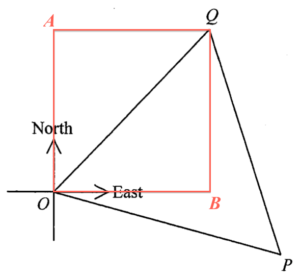
Add a rectangle on the figure as shown below.

Since the bearing of $P$ from $O$ is $\text{S}86^\circ\text{E}$ and the bearing of $Q$ from $O$ is $\text{N}32^\circ\text{E}$, we have
$\begin{array}{rcl}
\angle AOQ & = & 32^\circ
\end{array}$
and
$\begin{array}{rcl}
\angle POQ & = & 180^\circ – 32^\circ – 86^\circ \\
& = & 62^\circ
\end{array}$
Since $OP=OQ$, $\angle OQP = \angle OPQ$. Hence, we have
$\begin{array}{rcl}
\angle OQP & = & \dfrac{1}{2} (180^\circ – 62^\circ) \\
& = & 59^\circ
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\angle BQP & = & 59^\circ – 32^\circ \\
& = & 27^\circ
\end{array}$
Hence, the bearing of $P$ from $Q$ is $\text{S}27^\circ\text{E}$.

