2013-II-39

Ans: A
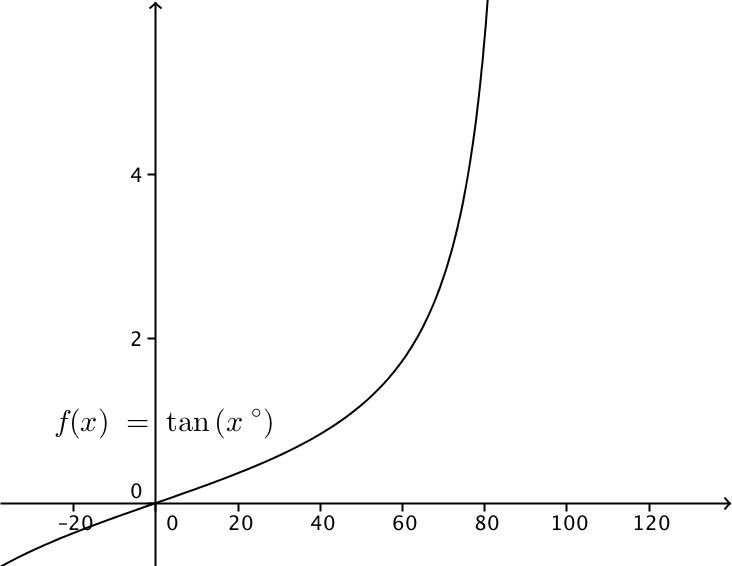
Consider the graph of $y=\tan x^\circ$.

By comparing the graphs of $y=\tan x^\circ$ and $y=h+k\tan2x^\circ$, we know that the graph is first reflected about $x$-axis and then translated upwards $2$ units. Hence, $k<0$ and $h=2$. Hence, I and II are true.

III is false. Sub. $x=\dfrac{\alpha^\circ}{2}$ into $y=2+k\tan 2x^\circ$, we have

$\begin{array}{rcl}
y & = & 2 + k \tan (2\times\dfrac{\alpha^\circ}{2}) \\
& = & 2+k\tan \alpha^\circ
\end{array}$

If $\tan \alpha^\circ =\dfrac{1}{k}$, then we have

$\begin{array}{rcl}
y & = & 2 + k \times\dfrac{1}{k} \\
& = & 3
\end{array}$

That means the graph $y=2+k\tan 2x^\circ$ passes through $(\tan \dfrac{\alpha^\circ}{2}, 3)$. Therefore, III is false.