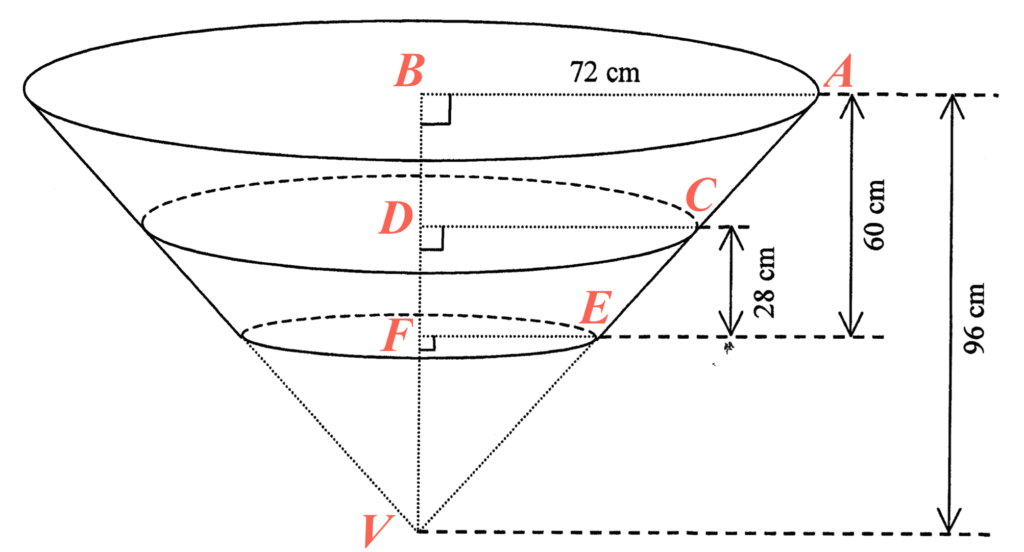
- Note that $\Delta VAB \sim \Delta VCD$. Hence, we have
$\begin{array}{rcl}
\dfrac{VB}{VD} & = & \dfrac{AB}{CD} \\
\dfrac{96}{96-60+28} & = & \dfrac{72}{CD} \\
CD & = & \dfrac{72 \times 64}{96} \\
& = & 48\text{ cm}
\end{array}$Therefore, we have
$\begin{array}{rcl}
VC & = & \sqrt{ VD^2 + CD^2} \\
& = & \sqrt{64^2 + 48^2} \\
& = & 80 \text{ cm}
\end{array}$Note also that $\Delta VAB \sim \Delta VEF$. Hence, we have
$\begin{array}{rcl}
\dfrac{VB}{VF} & = & \dfrac{AB}{EF} \\
\dfrac{96}{96 – 60} & = & \dfrac{72}{EF} \\
EF & = & \dfrac{72 \times 36}{96} \\
& = & 27 \text{ cm}
\end{array}$Therefore, we have
$\begin{array}{rcl}
VE & = & \sqrt{VF^2 + EF^2} \\
& = & \sqrt{36^2 + 27^2} \\
& = & 45 \text{ cm}
\end{array}$Hence, the area of the wet curved surface of the vessel
$\begin{array}{cl}
= & \pi (CD)(VC) – \pi (EF)(VE) \\
= & \pi \times 48 \times 80 – \pi \times 27 \times 45 \\
= & 2\ 625\pi \text{ cm}^2
\end{array}$ - The volume of water in the vessel
$\begin{array}{cl}
= & \dfrac{1}{3} \pi (CD)^2 (VD) – \dfrac{1}{3} \pi (EF)^2 (VF) \\
= & \dfrac{1}{3} \pi \times 48^2 \times 64 – \dfrac{1}{3} \pi \times 27^2 \times 36 \\
= & 40\ 404\pi \text{ cm}^3 \\
\approx & 126\ 932.909\ 6 \text{ cm}^3 \\
\approx & 0.126\ 932\ 909\ 6 \text{ m}^3 \\
> & 0.1 \text{ m}^3
\end{array}$Therefore, I agree with the claim.

