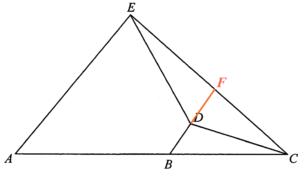
$BD$ is produced and intersects $EC$ at $F$. Note that $BF//AE$ and $\Delta ACE \sim \Delta BCF$. Hence we have
$\begin{array}{rcl}
AC:BC & = & EC:FC \\
& = & 5:2
\end{array}$
Therefore, $EF:FC = 3:2$.
If $CF$ and $EF$ are bases of $\Delta CDF$ and $\Delta EDF$ respectively, the two triangles have the same height. Therefore, the area of $\Delta CDF$
$\begin{array}{cl}
= & 8 \times \dfrac{2}{3+2} \\
= & 3.2 \text{ cm}^2
\end{array}$
Since $\Delta ACE \sim \Delta BCF$, then we have
$\begin{array}{rcl}
\dfrac{\text{area of $\Delta BCF$}}{\text{area of $\Delta ACE$}} & = & \left(\dfrac{BC}{AC}\right)^2 \\
\dfrac{3.2 + 4}{\text{area of $\Delta ACE$}} & = & \left(\dfrac{2}{5}\right)^2 \\
\text{area of $\Delta ACE$} & = & 45 \text{ cm}^2
\end{array}$
Hence, the area of the trapezium $ABDE$
$\begin{array}{cl}
= & 45 – 4 – 8 \\
= & 33 \text{ cm}^2
\end{array}$

