Ans: A
Since $AB=CD=EF$, then the distances between the centre $O$ and the three chords $AB$, $CD$ and $EF$ are the same. Hence, we can draw a circle inscribed in $\Delta PQR$ as shown in the following figure.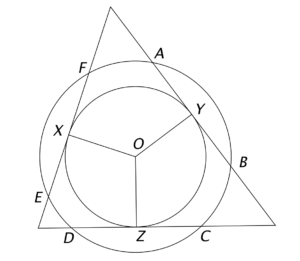
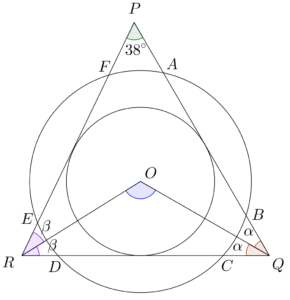
Since $AB=CD=EF$, then the distances between the centre $O$ and the three chords $AB$, $CD$ and $EF$ are the same. Hence, we can draw a circle inscribed in $\Delta PQR$ as shown in the following figure.

Note that $PQ$, $QR$ and $PR$ are tangents to the smaller circle. Then by the tangent properties, we have
$\begin{array}{rcl}
\angle QOP & = & \angle OQR \\
\angle ORQ & = & \angle ORP
\end{array}$

Consider $\Delta PQR$, we have
$\begin{array}{rcl}
2\alpha + 2\beta + 38^\circ & = & 180^\circ \\
\alpha + \beta & = & 71^\circ
\end{array}$
Consider $\Delta ORQ$, we have
$\begin{array}{rcl}
\angle QOR & = & 180^\circ – \beta – \alpha \\
\angle QOR & = & 180^\circ – (\beta + \alpha) \\
\angle QOR & = & 180^\circ – 71^\circ \\
\angle QOR & = & 109^\circ
\end{array}$

