Ans: D
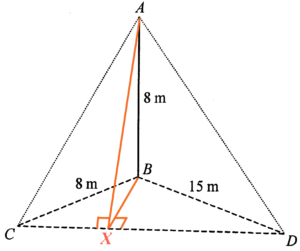

Note that $\angle AXB = \theta$. Consider $\Delta BCD$, by the Pythagorus Theorem, we have
$\begin{array}{rcl}
CD & = & \sqrt{8^2 + 15^2} \\
& = & 17
\end{array}$
Hence, we have
$\begin{array}{rcl}
\sin \angle BCD & = & \dfrac{15}{17}
\end{array}$
Consider $\Delta BCX$,
$\begin{array}{rcl}
\sin \angle BCD & = & \dfrac{BX}{8} \\
BX & = & 8 \sin \angle BCD \\
BX & = & 8 \times \dfrac{15}{17} \\
BX & = & \dfrac{120}{17}
\end{array}$
Consider $\Delta ABX$,
$\begin{array}{rcl}
\tan \theta & = & \dfrac{AB}{BX} \\
\tan \theta & = & \dfrac{8}{ \frac{120}{17}} \\
\tan \theta & = & \dfrac{17}{15}
\end{array}$

