2015-I-19

1. By applying the cosine law to $\Delta ABC$, we have

   $\begin{array}{rcl}
   AC^2 & = & AB^2 + BC^2 – 2(AB)(AC)\cos \angle ABC \\
   AC^2 & = & (40)^2 + (24)^2 -2(40)(24) \cos \angle 80^\circ \\
   AC & = & 42.925\ 464\ 46
   \end{array}$

   Therefore, the distance between $A$ and $C$ is $42.9\text{ cm}$.

2. By applying the sine law to $\Delta ABC$, we have

   $\begin{array}{rcl}
   \dfrac{AB}{\sin \angle ACB} & = & \dfrac{AC}{\sin \angle ABC} \\
   \dfrac{40}{\sin \angle ACB} & = & \dfrac{42.925\ 464\ 46}{\sin 80^\circ} \\
   \sin \angle ACB & = & \dfrac{40\sin 80^\circ}{42.925\ 464\ 46} \\
   \sin \angle ACB & = & 0.917\ 690\ 926 \\
   \angle ACB & = & 66.590\ 814\ 87^\circ \\
   \angle ACB & \approx & 66.6^\circ
   \end{array}$

3. Join $AC$ and $AD$.
   

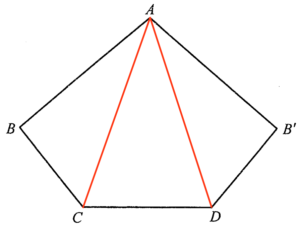
   It is obviously that the paper card consists of three parts, $\Delta ABC$, $\Delta ACD$ and $\Delta AB’D$. Since $AB=AB’=40$, $BC= B’D=24$ and $\angle ABC = \angle AB’D=80^\circ$, then $\Delta ABC \cong \Delta AB’D$. The area of $\Delta ABC$

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times AB \times BC \times \sin \angle ABC \\
   = & \dfrac{1}{2} \times 40 \times 24 \times \sin 80^\circ \\
   = & 480\sin80^\circ \text{ cm}^2
   \end{array}$

   Since $AC=AD$, then the area of $\Delta ACD$

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times AC \times AD \times \sin \angle CAD \\
   = & \dfrac{1}{2} \times 42.925\ 464\ 46^2 \times \sin \angle CAD \\
   = & 921.297\ 749\ 4 \sin \angle CAD \text{ cm}^2
   \end{array}$

   Therefore, the area of the paper card

   $\begin{array}{cl}
   = & 2 \times 480 \sin 80^\circ + 921.297\ 749\ 4 \sin \angle CAD \\
   = & 960 \sin 80^\circ + 921.297\ 749\ 4 \sin \angle CAD
   \end{array}$

   Hence, the greater the value of $\sin \angle CAD$, the greater the area of the paper card.

   Note that $AC=AD$, then $\angle ACD = \angle ADC$.

   $\begin{array}{rcl}
   \angle CAD & = & 180^\circ – 2 \times \angle ACD \\
   \angle CAD & = & 180^\circ – 2 \times (\angle BCD – \angle ACB) \\
   \angle CAD & = & 180^\circ – 2\angle BCD + 2(66.590\ 814\ 87^\circ) \\
   \angle CAD & = & 313.181\ 629\ 7^\circ – 2\angle BCD
   \end{array}$

   Since $105^\circ \le \angle BCD \le 145^\circ$, then we have
   

   $23.181\ 629\ 74^\circ \le \angle CAD \le 103.181\ 629\ 7^\circ$.

   Therefore, the value of $\sin \angle CAD$ attains its maximum when $\angle CAD = 90^\circ$. Hence, the area of the paper card attains its maximum when $\angle CAD = 90^\circ$. For $\angle CAD = 90^\circ$, $\angle ACD = 45^\circ$. Therefore, the area of the paper card attains its maximum when $\angle BCD$

   $\begin{array}{cl}
   = & 45^\circ + \angle ACB \\
   = & 45^\circ + 66.590\ 814\ 87^\circ \\
   = & 111.590\ 814\ 9^\circ
   \end{array}$

   Hence, we can draw a conclusion:

   When $\angle BCD$ increases from $105^\circ$ to $111.590\ 814\ 9^\circ$, the area of the paper card increases. And when $\angle BCD$ increases from $111.590\ 814\ 9^\circ$ to $145^\circ$, the area of the paper card decreases.

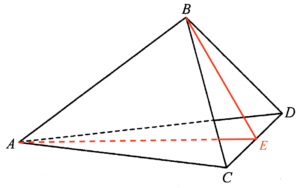
Consider $\Delta ACE$,

$\begin{array}{rcl}
\angle ACD & = & \angle BCD – \angle ACB \\
\angle ACD & = & 132^\circ – 66.590\ 814\ 87^\circ \\
\angle ACD & = & 65.409\ 185\ 513^\circ
\end{array}$

Since $AC=AD$ and $E$ is the mid-point of $CD$, then $\angle AEC$ is a right-angle. Hence, we have

$\begin{array}{rcl}
\cos \angle ACE & = & \dfrac{CE}{AC} \\
CE & = & AC \cos \angle ACE \\
CE & = & 42.925\ 464\ 46 \cos 65.409\ 185\ 513^\circ \\
CE & = & 17.862\ 789\ 29 \text{ cm}
\end{array}$

and

$\begin{array}{rcl}
\sin \angle ACE & = & \dfrac{AE}{AC} \\
AE & = & AC \sin \angle ACE \\
AE & = & 42.925\ 464\ 46 \sin 65.409\ 185\ 513^\circ \\
AE & = & 39.032\ 246\ 38\text{ cm}
\end{array}$

Consider $\Delta BCE$. Since $BC = BD$ and $E$ is the mid-point of $CD$, then $\angle BEC$ is a right-angle. By applying the Pythagoras Theorem to $\Delta BCD$, we have

$\begin{array}{rcl}
BE^2 & = & BC^2 – CE^2 \\
BE & = & \sqrt{24^2 – (17.862\ 789\ 29)^2} \\
BE & = & 16.028\ 747\ 88 \text{ cm}
\end{array}$

Consider $\Delta ABE$. By applying the cosine law to $\Delta ABE$, we have

$\begin{array}{rcl}
\cos \angle AEB & = & \dfrac{AE^2 + BE^2 – AB^2}{2(AE)(BE)} \\
\cos \angle AEB & = & 0.144\ 202\ 402 \\
\angle AEB & = & 81.708\ 905\ 17^\circ
\end{array}$

Let $X$ be the foot of perpendicular of $B$ on the plane $ACD$. Since $\Delta ABC \cong \Delta ABD$, then $X$ lies on $AE$.

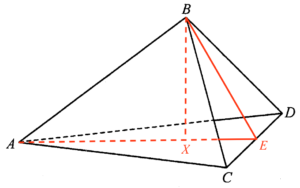
Consider $\Delta BXE$. Note that $\angle BXE$ is a right-angle. Hence, we have

$\begin{array}{rcl}
\sin \angle BEX & = & \dfrac{BX}{BE} \\
BX & = & BE \sin \angle BEX \\
BX & = & 16.028\ 747\ 88 \sin 81.708\ 905\ 17^\circ \\
BX & = & 15.861\ 218\ 83 \text{ cm}
\end{array}$

Hence, the volume of the pyramid $ABCD$

$\begin{array}{cl}
= & \dfrac{1}{3} \times \text{ the area of $\Delta ACD$} \times BX \\
= & \dfrac{1}{3} \times \dfrac{1}{2} \times CD \times AE \times BX \\
= & 3686.278\ 337 \text{ cm}^3 \\
\approx & 3690 \text{ cm}^3
\end{array}$