Since $BD$ is a diameter of the circle, then we have
$\begin{array}{ll}
BD\perp AB & \text{(radius $\perp$ tangent)}
\end{array}$
Therefore, $\angle EBA=90^\circ$.
By applying the Pythagorus Theorem to $\Delta ABE$, we have
$\begin{array}{rcl}
AE^2 & = & AB^2 + BE^2 \\
10^2 & = & 6^2 + BE^2 \\
BE^2 & = & 64 \\
BE & = & 8 \text{ cm}
\end{array}$
Note that
$\begin{array}{ll}
AC = AB & \text{(tangent properties)} \\
AC = 6 \text{ cm}
\end{array}$
Therefore, $EC = 4 \text{ cm}$.
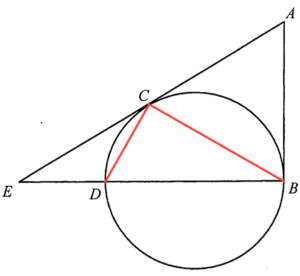
Join $BC$ and $CD$. Consider $\Delta BCE$ and $\Delta CDE$.
$\begin{array}{rcll}
\angle CEB & = & \angle DEC & \text{(common $\angle$)} \\
\angle CBE & = & \angle DCE & \text{($\angle$s in alt. segment)} \\
\angle BCE & = & 180^\circ – \angle CEB – \angle BCE & \text{($\angle$ sum of $\Delta$)} \\
& = & 180^\circ \angle DEC – \angle DCE & \text{(proved)} \\
& = & \angle CDE & \text{($\angle$ sum of $\Delta$)}
\end{array}$
Therefore, $\Delta BCE\sim \Delta CDE \text{ (A.A.A.)}$.
Hence, we have
$\begin{array}{rcll}
\dfrac{BE}{CE} & = & \dfrac{CE}{DE} & \text{(corr. sides, $\sim \Delta$s)} \\
\dfrac{8}{4} & = & \dfrac{4}{DE} \\
DE & = & 2 \text{ cm}
\end{array}$
Therefore, we have
$\begin{array}{rcl}
BD & = & BE – DE \\
& = & 8 – 2 \\
& = & 6 \text{ cm}
\end{array}$

