2016-I-20

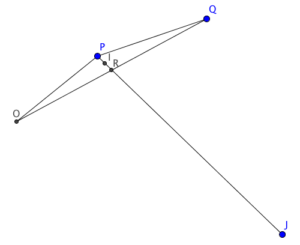
Consider $\Delta PRO$ and $\Delta PRQ$.

Since $I$ is the in-centre of $\Delta OPQ$, then $PI$ is the angle bisector of $\angle OPQ$. Hence, we have

$\begin{array}{ll}
\angle RPO = \angle RPQ & \text{(in-centre)}
\end{array}$

Since $J$ is the circumcentre of $\Delta OPQ$, then $PJ$ is the perpendicular bisector of $OQ$. Hence, we have

$\begin{array}{ll}
\angle PRO = \angle PRQ = 90^\circ & \text{(circumcentre)} \\
RO = RQ & \text{(circumcentre)}
\end{array}$

Therefore, $\Delta PRO \cong \Delta PRQ$ (A.A.S). Hence, we have

$\begin{array}{ll}
OP = PQ & \text{(corr. sides, $\cong \Delta$)}
\end{array}$

1. Refere to the figure below.
   

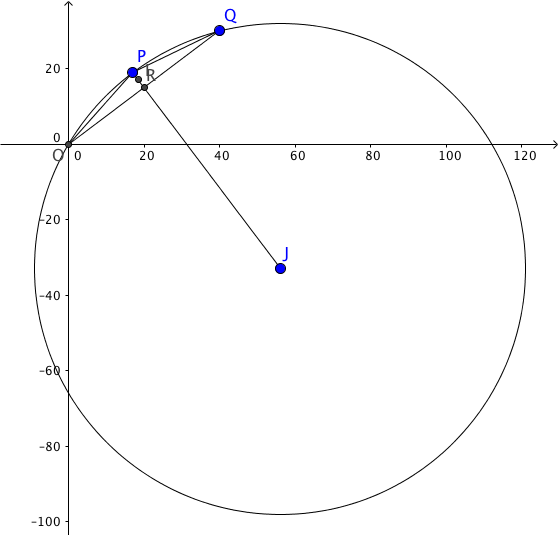
   Let $P=(a, 19)$. By the result of (a), $OP=PQ$. Hence, we have

   $\begin{array}{rcl}
   \sqrt{(a-0)^2 + (19-0)^2} & = & \sqrt{(a-40)^2 + (19-30)^2} \\
   a^2 + 361 & = & a^2 -80a + 1721 \\
   80a & = & 1360 \\
   a & = & 17
   \end{array}$

   Let $x^2+y^2+Dx+Ey+F=0$ be the equation of $C$. Since $C$ passes through $O$, $P$ and $Q$, we have

   $\left\{ \begin{array}{ll}
   (0)^2 + (0)^2 +D(0) + E(0) + F =0 & \ldots \unicode{x2460} \\
   17^2 + 19^2 + D(17) + E(19) + F = 0 & \ldots \unicode{x2461} \\
   40^2 + 30^2 +D(40) + E(30) + F = 0 & \ldots \unicode{x2462}
   \end{array} \right.$

   From $\unicode{x2460}$, we have $F=0$. Then after simplifying $\unicode{x2461}$ and $\unicode{x2462}$, we have

   $\left\{ \begin{array}{ll}
   17D + 19E + 650 =0 & \ldots \unicode{x2463} \\
   40D + 30E + 2500 = 0 & \ldots \unicode{x2464}
   \end{array} \right.$

   $\unicode{x2463} \times 30 – \unicode{x2464} \times 19$, we have

   $\begin{array}{rcl}
   -250D -28000 & = & 0 \\
   D & = & -112
   \end{array}$

   Sub. $D=-112$ into $\unicode{x2463}$, we have

   $\begin{array}{rcl}
   17(-112) + 19E + 650 & = & 0 \\
   19E & = & 1254 \\
   E & = & 66
   \end{array}$

   Hence, the equation of $C$ is $x^2 +y^2 -112x +66y=0$.

2. Refer to the figure below.
   

   Let $y=\dfrac{3}{4}x + c$ be the tangent to $C$ with slope $\dfrac{3}{4}$. Sub. $y= \dfrac{3}{4}x +c$ into the equation of $C$, we have

   $\begin{array}{rcl}
   x^2 + (\dfrac{3}{4}x+c)^2 -112x +66(\dfrac{3}{4}x+c) & = & 0 \\
   x^2 + \dfrac{9}{16}x^2 + \dfrac{3c}{2}x +c^2 -112x + \dfrac{99}{2} x + 66c & = & 0 \\
   16x^2 + 9x^2 + 24cx + 16c^2 – 1792x + 792 x + 1056c & = & 0 \\
   25x^2 + (24c-1000)x + (16c^2 + 1056c) & = & 0
   \end{array}$

   Since $y=\dfrac{3}{4}x +c$ is a tangent to $C$, then we have

   $\begin{array}{rcl}
   \Delta & = & 0 \\
   (24c-1000)^2 – 4(25)(16c^2 +1056c) & = & 0 \\
   576c^2 – 48000c + 1000000 – 1600c^2 – 105600c & = & 0 \\
   1024c^2 + 153600c – 1000000 & = & 0 \\
   16c^2 + 2400c – 15625 & = & 0 \\
   (4c -25)(4c+625) & = & 0
   \end{array}$

   Therefore, $c=\dfrac{25}{4}$ or $c=\dfrac{-625}{4}$.

   Therefore, the equations of $L_1$ and $L_2$ are $y=\dfrac{3}{4}x + \dfrac{25}{4}$ and $y=\dfrac{3}{4}x -\dfrac{625}{4}$ respectively. Hence, the coordinates of $S$, $T$, $U$ and $V$ are $(\dfrac{-25}{3},0)$, $(0,\dfrac{25}{4})$, $(\dfrac{625}{3},0)$ and $(0,\dfrac{-625}{4})$ respectively.

   Note that the height of the trapezium $STUV$ is the diameter of the circle $C$. Then the height of the trapezium $STUV$

   $\begin{array}{cl}
   = & \sqrt{(\dfrac{112}{2})^2 + (\dfrac{66}{2})^2 – 0} \\
   = & 65
   \end{array}$

   Therefore, the area of the trapezium $STUV$

   $\begin{array}{cl}
   = & \dfrac{2\times 65}{2} \left[ \sqrt{(\dfrac{-25}{3}-0)^2 + (0-\dfrac{25}{4})^2} + \sqrt{(\dfrac{625}{3} – 0)^2 + (0- \dfrac{-625}{4})^2} \right] \\
   = & \dfrac{105625}{6} \\
   > & 17000
   \end{array}$

   Therefore, the claim is correct.