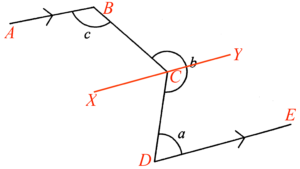
Add a straight line $DE$ passing through $C$ such that $AB\text{//}XY\text{//}DE$.
I may not be true.
$\angle BCY = c$ (alt. $\angle$s, $AB$//$XY$)
$\angle XCD = a$ (alt. $\angle$s, $XY$//$DE$)
If $\angle BCX = a$, then we have
$a + c = 180^\circ$ (adj. $\angle$s on a st. line).
However, $\angle BCX$ may not equal to $a$. Therefore I may not be true.
II must be true.
$\angle BCY = c$ (alt. $\angle$s, $AB$//$XY$)
$\angle XCD = a$ (alt. $\angle$s, $XY$//$DE$)
$\begin{array}{cl}
& a + b – c \\
= & \angle XCD + \text{reflex } \angle BCD – \angle BCY \\
= & \angle XCY \\
= & 180^\circ
\end{array}$
Hence, II must be true.
III may not be true.
$\angle BCX = 180^\circ- c$ (int. $\angle$s, $AB$//$XY$)
$\angle XCD = a$ (alt. $\angle$s, $XY$//$DE$)
If $a = 2c + 180^\circ$, then we have
$\begin{array}{rcl}
\angle BCD & = & 180^\circ – c + a \\
\angle BCD & = & 180^\circ – c + (2c +180^\circ) \\
\angle BCD & = & c
\end{array}$
Therefore,
$b + c = 360^\circ$ ($\angle$s at a pt)
However, $a$ may not equal to $2c + 180^\circ$.
Hence, III may not be true.

