Ans: C
Add a point $E$ on $CD$ such that $BE\perp CD$.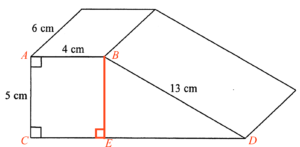
Add a point $E$ on $CD$ such that $BE\perp CD$.

Since $ABEC$ is a rectangle, then $BE = 5\text{ cm}$ and $CE=4\text{ cm}$.
By using Pythagoras Theorem on $\Delta BDE$, we have
$\begin{array}{rcl}
DE^2 + BE^2 & = & BD^2 \\
DE^2 + (5)^2 & = & (13)^2 \\
DE & = & \sqrt{169 – 25} \\
DE & = & 12 \text{ cm}
\end{array}$
Therefore, the base area of the prism
$\begin{array}{cl}
= & \dfrac{1}{2} \times [ 4 + (4+12)] \times 5 \\
= & 50 \text{ cm}^2
\end{array}$
Hence, the volume of the prism
$\begin{array}{cl}
= & 50 \times 6 \\
= & 300 \text{ cm}^3
\end{array}$

