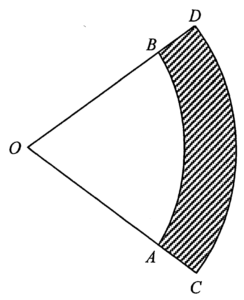
I is true. Let $\theta$ be the angle of the sector $OAB$. Consider the area of the shaded region $ABDC$.
$\begin{array}{rcl}
\pi (OC)^2 \times \dfrac{\theta}{360^\circ} – \pi (OA)^2 \times \dfrac{\theta}{360^\circ} & = & 72 \pi \\
\pi (39)^2 \times \dfrac{\theta}{360^\circ} – \pi (33)^2 \times \dfrac{\theta}{360^\circ} & = & 72 \pi \\
432\theta & = & 25920^\circ \\
\theta & = & 60^\circ
\end{array}$
II is not true. By the result of I, $\theta = 60^\circ$. Therefore, the area of the sector $OAB$
$\begin{array}{cl}
= & \pi (33)^2 \times \dfrac{60^\circ}{360^\circ} \\
= & 181.5\pi \text{ cm}^2
\end{array}$
III is not true. By the result of I, $\theta = 60^\circ$. Therefore, the perimeter of the sector $OCD$
$\begin{array}{cl}
= & 2\pi(39) \times \dfrac{60^\circ}{360^\circ} + 2 (39) \\
= & (13 \pi + 78) \text{ cm}
\end{array}$

