Ans: B
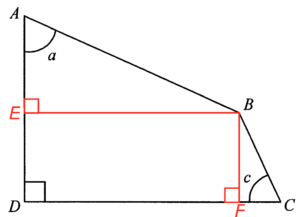

Add points $E$ and $F$ on $AD$ and $CD$ respectively, such that $BE \perp AD$ and $BF \perp CD$.
Consider $\Delta ABE$, we have
$\begin{array}{rcl}
\cos a & = & \dfrac{AE}{AB} \\
AE & = & AB \cos a
\end{array}$
Consider $\Delta BCF$, we have
$\begin{array}{rcl}
\sin c & = & \dfrac{BF}{BC} \\
BF & = & BC \sin c
\end{array}$
Note that $BEDF$ is a rectangle, therefore $ED = BF$. Hence, we have
$\begin{array}{rcl}
AD & = & AE + ED \\
& = & AB \cos a + BC \sin c
\end{array}$

