Ans: D
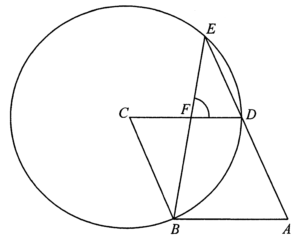

Since $ABCD$ is a rhombus, then we have $BC\text{//}AD$.
$\begin{array}{rcll}
\angle BCD + \angle ADC & = & 180^\circ & \text{(int. $\angle$s, $BC$//$AD$)} \\
\angle BCD + 118^\circ & = & 180^\circ & \\
\angle BCD & = & 62^\circ
\end{array}$
Therefore, we have
$\begin{array}{rcll}
\angle BED & = & \dfrac{1}{2} \times \angle BCD & \text{($\angle$ at centre twice $\angle$ at $\unicode{x2299}^{ce}$)} \\
\angle BED & = & \dfrac{1}{2} \times 62^\circ & \\
\angle BED & = & 31^\circ & \\
\end{array}$
Consider $\Delta DEF$.
$\begin{array}{rcll}
\angle DEF & = & \angle ADC – \angle BED & \text{(ext. $\angle$ of $\Delta$)} \\
\angle DEF & = & 118^\circ – 31^\circ & \\
\angle DEF & = & 87^\circ
\end{array}$

