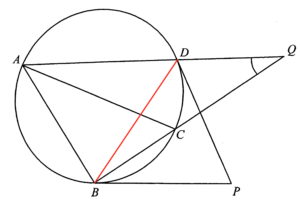
Join $BD$. Consider $\Delta PBD$, we have
$\begin{array}{rcll}
PD & = & PB & \text{(tangent properties)} \\
\angle PDB & = & \angle PBD & \text{(base $\angle$s, isos. $\Delta$)} \\
\angle PDB & = & \dfrac{1}{2} \times (180^\circ – \angle AQB) & \text{($\angle$ sum of $\Delta$)} \\
\angle PDB & = & \dfrac{1}{2} \times (180^\circ – 68^\circ) & \\
\angle PDB & = & 56^\circ
\end{array}$
Consider $\Delta ABD$, we have
$\begin{array}{rcll}
\angle BAD & = & \angle PDB & \text{($\angle$s in alt. segment)} \\
\angle BAD & = & 56^\circ
\end{array}$
Consider $\Delta ABQ$,
$\begin{array}{rcll}
\angle ABQ & = & 90^\circ & \text{($\angle$ in semi circle)} \\
\angle AQB & = & 180^\circ – \angle BAD – \angle ABQ & \text{($\angle$ sum of $\Delta$)} \\
\angle AQB & = & 180^\circ – 90^\circ – 56^\circ & \\
\angle AQB & = & 34^\circ
\end{array}$

