2017-I-19

$\begin{array}{rcl}
\dfrac{AC}{\sin \angle ABC} & = & \dfrac{BC}{\sin \angle BAC} \\
\dfrac{AC}{\sin (180^\circ – 30^\circ-42^\circ)} & = & \dfrac{24}{\sin 30^\circ} \\
AC & = & 45.650\ 712\ 78 \text{ cm}
\end{array}$

1. Join $D$, $E$ and $F$. Note that $DEF$ is a straight line.
   

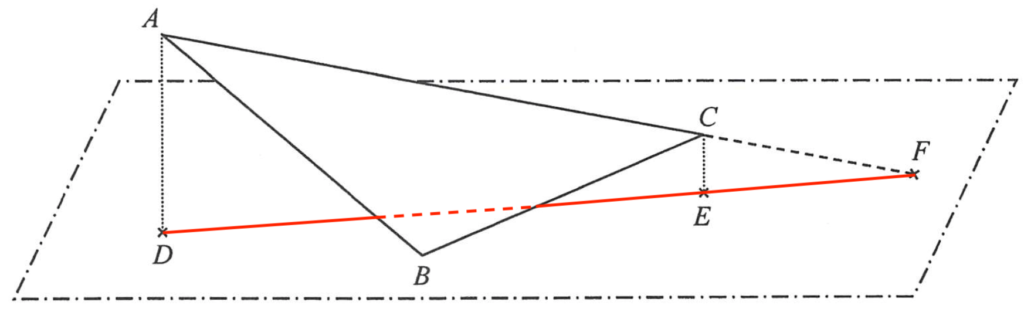
   Since $D$ and $E$ are points lying on the horizontal ground vertically below the vertices $A$ and $C$ respectively, then $\Delta ADF \sim \Delta CEF$. Therefore, we have

   $\begin{array}{rcl}
   \dfrac{AD}{CD} & = & \dfrac{AF}{CF} \\
   \dfrac{10}{2} & = & \dfrac{AC + CF}{CF} \\
   10 CF & = & 2AC + 2CF \\
   8CF & = & 2AC \\
   CF & = & 11.412\ 678\ 2\text{ cm}
   \end{array}$

2. Note that the height of $\Delta ABC$ and that of $\Delta ABF$ are the same. Therefore, the height of $\Delta ABF$

   $\begin{array}{cl}
   = & BC \times \sin \angle BCA \\
   = & 24 \times \sin 42^\circ \text{ cm}
   \end{array}$

   $\therefore$ the area of $\Delta ABF$

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times AF \times \text{the height of } \Delta ABF \\
   = & \dfrac{1}{2}\times ( 45.650\ 712\ 78 + 11.412\ 678\ 2) \times (24 \times \sin 42^\circ) \\
   = & 458.194\ 336\ 9\text{ cm}^2
   \end{array}$

3. Join $FB$. Extend $FB$ to point $X$ such that $AX \perp FB$ and $DX \perp FB$.
   

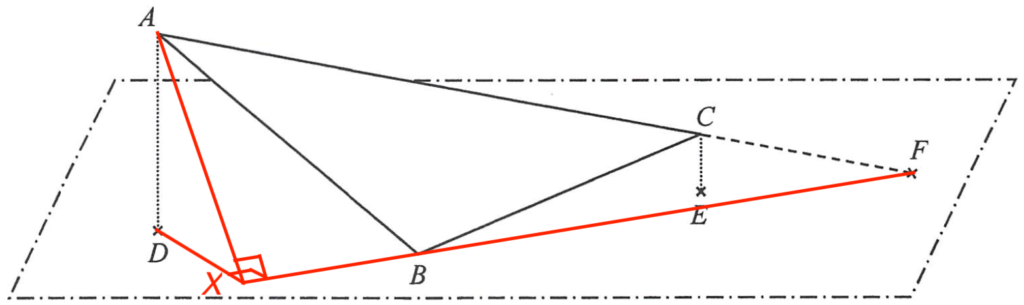
   Note that the required angle is $\angle AXD$.

   By applying cosine law to $\Delta BCF$, we have

   $\begin{array}{rcl}
   BF^2 & = & CF^2 +BC^2 -2(BC)(BF)\cos \angle BCF \\
   BF^2 & = & (11.412\ 678\ 2)^2 +24^2 – 2(11.412\ 678\ 2)(24) \cos (180^\circ – 42^\circ) \\
   BF & = & 33.366\ 904\ 449\text{ cm}
   \end{array}$

   Note that $AX$ is the height of $\Delta ABF$ with base $BF$. Therefore, by the result of (b)(ii), we have

   $\begin{array}{rcl}
   \dfrac{1}{2} \times AX \times BF & = & \text{the area of }\Delta ABF \\
   \dfrac{1}{2} \times AX \times 33.366\ 904\ 449 & = & 458.194\ 336\ 9 \\
   AX & = & 27.464\ 000\ 26 \text{ cm}
   \end{array}$

   Consider $\Delta ADX$,

   $\begin{array}{rcl}
   \sin \angle AXD & = & \dfrac{AD}{AX} \\
   \sin \angle AXD & = & \dfrac{10}{27.464\ 000\ 26} \\
   \angle AXD & = & 21.353\ 006\ 46^\circ
   \end{array}$

   Therefore, the inclination of the thin metal sheet $ABC$ to the horizontal ground is $21.4^\circ$.

4. Join $BD$ and $DF$.
   

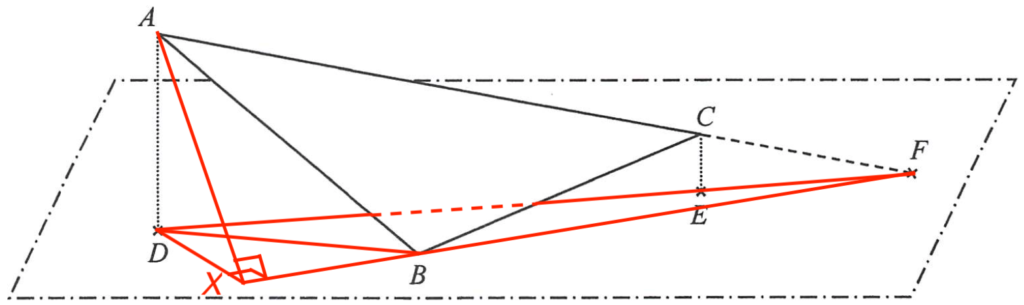
   Note that $DX$ is the height of $\Delta BDF$ with base $BF$. Therefore, the area of $\Delta BDF$

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times DX \times BF \\
   = & \dfrac{1}{2} \times \dfrac{AD}{\tan \angle AXD} \times BF \\
   = & \dfrac{1}{2} \times \dfrac{10}{\tan 21.353\ 006\ 46^\circ} \times 33.366\ 904\ 449 \\
   = & 426.741\ 482\text{ cm}^2 \\
   < & 460\text{ cm}^2 \end{array}$

   Hence, I don’t agree with the craftsman’s claim.