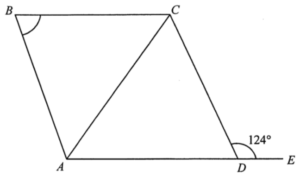
Consider $\Delta ACD$,
$\begin{array}{rcl}
\angle ADC & = & 180^\circ – 124^\circ \ \text{(adj. $\angle$s on a st. line)} \\
\angle ADC & = & 56^\circ
\end{array}$
Since $AC = AD$, then we have
$\begin{array}{rcl}
\angle ACD & = & \angle ADC \ \text{(base $\angle$, isos. $\Delta$)} \\
\angle ACD & = & 56^\circ
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\angle CAD & = & 180^\circ – \angle ADC – \angle ACD \ \text{($\angle$ sum of $\Delta$)} \\
\angle CAD & = & 180^\circ – 56^\circ – 56^\circ \\
\angle CAD & = & 68^\circ
\end{array}$
Since $AE\text{//}BC$, then we have
$\begin{array}{rcl}
\angle BCA & = & \angle CAD \ \text{(alt. $\angle$s, $AE$//$BC$)} \\
\angle BCA & = & 68^\circ
\end{array}$
Consider $\Delta ABC$. Since $AB=BC$, we have
$\begin{array}{rcl}
\angle BAC & = & \angle BCA \ \text{(base $\angle$, isos. $\Delta$)} \\
\angle BAC & = & 68^\circ
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\angle ABC & = & 180^\circ – \angle BAC – \angle BCA \ \text{($\angle$ sum of $\Delta$)} \\
\angle ABC & = & 180^\circ – 68^\circ – 68^\circ \\
\angle ABC & = & 44^\circ
\end{array}$

