Add a straight line $XZ$ passing through $A$ such that $XZ \perp GH$ and $XZ \perp FE$. $XZ$ intersects $CD$ at $Y$ and $XZ \perp CD$. $AB$ produced cuts $GF$ and $DE$ at $P$ and $Q$ respectively. Note that $PQ \perp GF$ and $PQ \perp DE$.
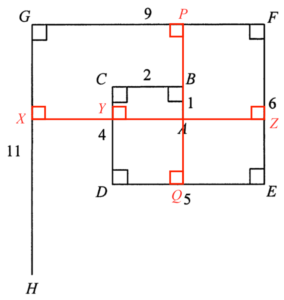
Since $ABCY$ is a rectangle, then $CY = AB = 1$. Hence, we have
$\begin{array}{rcl}
DY & = & CD – CY \\
DY & = & 4 -1 \\
DY & = & 3
\end{array}$
Since $DEZY$ is a rectangle, then $DY = EZ = 3$. Hence, we have
$\begin{array}{rcl}
FZ & = & EF – EZ \\
FZ & = & 6 – 3 \\
DY & = & 3
\end{array}$
Since $XZFG$ is a rectangle, then $FZ = GX = 3$. Hence, we have
$\begin{array}{rcl}
XH & = & GH – GX \\
XH & = & 11 – 3 \\
XH & = & 8
\end{array}$
Since $BCDQ$ is a rectangle, then $BC = DQ = 2$. Hence, we have
$\begin{array}{rcl}
QE & = & DE – DQ \\
QE & = & 5 – 2 \\
QE & = & 3
\end{array}$
Since $PQEF$ is a rectangle, then $QE = PF = 3$. Hence, we have
$\begin{array}{rcl}
GP & = & GF – PF \\
GP & = & 9 – 3 \\
GP & = & 6
\end{array}$
Since $PGXA$ is a rectangle, then $GP = XA = 6$.
By applying the Pythagoras Theorem to $\Delta AXH$, we have
$\begin{array}{rcl}
AH^2 & = & XH^2 + XA^2 \\
AH^2 & = & (8)^2 + (6)^2 \\
AH^2 & = & 100 \\
AH & = & 10
\end{array}$

