According to the question, we draw the parallelogram first.
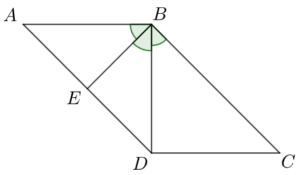
I is true. Since $ABCD$ is a parallelogram, then $AD//BC$.
In $\Delta EBD$,
$\angle BDA = \angle DBC$ (alt. $\angle$s, $AD//DC$)
$\therefore EB=ED$ (sides opp. eq. $\angle$s)
In $\Delta EBA$,
$ED = EA$ ($E$ is the mid-pt of $AD$)
$\therefore EA = EB$.
Hence, we have $\angle EAB = \angle EBA$ (base $\angle$s, isos. $\Delta$).
In $\Delta BAD$,
$\because \angle BAD = \angle ABE$, $\angle ABE = \angle CBD$ and $\angle CBD = \angle BDE$,
$\therefore \angle BAD = \angle BDA$.
$\therefore AB = BD$ (sides opp. eq. $\angle$s).
II is true. Since $\angle ABE = \angle DBE = \angle CBD = \angle BAD$ and $AD//BC$, we have
$\begin{array}{rcll}
\angle BAD + \angle ABC & = & 180^\circ & \text{(int. $\angle$s, $AD//BC$)} \\
\angle BAD + \angle ABE + \angle DBE + \angle CBD& = & 180^\circ \\
4\angle ABE & = & 180^\circ \\
\angle ABE & = & 45^\circ \\
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\angle ABC & = & 3 \times \angle ABE \\
& = & 3 \times 45^\circ \\
& = & 135^\circ
\end{array}$
III is true. In $\Delta ABE$ and $\Delta DBE$,
$\begin{array}{rcll}
BE & = & BE & \text{(common side)} \\
AB & = & DB & \text{(proved)} \\
AE & = & DE & \text{($E$ is the mid-pt of $AD$)}
\end{array}$
$\therefore \Delta ABD \cong \Delta DBE$ (S.S.S.).

