Join $AC$.
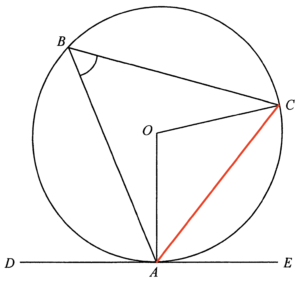
Since $DE$ is the tangent to the circle at $A$, then
$\begin{array}{rcll}
\angle BCA & = & \angle BAD & \text{($\angle$s in alt. segment)}\\
\angle BCA & = & 68^\circ
\end{array}$
Consider $\Delta OAC$.
$\begin{array}{rcl}
\angle OCA & = & \angle BCA – \angle BCO \\
\angle OCA & = & 68^\circ -26^\circ \\
\angle OCA & = & 42^\circ
\end{array}$
Since $OA = OC$ (radii), then $\angle OAC = \angle OCA$ (base $\angle$s, isos. $\Delta$). Hence, we have
$\begin{array}{rcll}
\angle AOC & = & 180^\circ – \angle OAC – \angle OCA & \text{($\angle$ sum of $\Delta$)} \\
\angle AOC & = & 180^\circ – 42^\circ – 42^\circ \\
\angle AOC & = & 96^\circ
\end{array}$
Hence, we have
$\begin{array}{rcll}
\angle ABC & = & \dfrac{1}{2} \times \angle AOC & \text{($\angle$ at centre twice $\angle$ at $\unicode{x2299}^{ce}$)} \\
\angle ABC & = & \dfrac{1}{2} \times 96^\circ \\
\angle ABC & = & 48^\circ
\end{array}$

