2018-I-17

$\begin{array}{rcll}
\angle ADB & = & 180^\circ – 120^\circ – 20^\circ \\
\angle ADB & = & 40^\circ
\end{array}$

By applying sine law to $\Delta ABD$, we have

$\begin{array}{rcl}
\dfrac{AB}{\sin \angle ADB} & = & \dfrac{AD}{\sin \angle ABD} \\
\dfrac{60}{\sin 40^\circ} & = & \dfrac{AD}{\sin20^\circ} \\
AD & = & 31.925\ 333\ 17\text{ cm}
\end{array}$

1. By applying cosine law to $\Delta ABC$, we have

   $\begin{array}{rcl}
   \cos \angle ABC & = & \dfrac{AB^2 + BC^2 – AC^2}{2\times AB \times BC} \\
   \cos \angle ABC & = & \dfrac{AB^2 + AD^2 – AC^2}{2\times AB \times AD} \\
   \cos \angle ABC & = & \dfrac{60^2 + 31.925\ 333\ 17^2 – 40^2}{2\times 60 \times 31.925\ 333\ 17} \\
   \cos \angle ABC & = & 0.788\ 095\ 899 \\
   \angle ABC & = & 37.992\ 075\ 34^\circ
   \end{array}$

2. Add a point $X$ on $BD$ such that $AX \perp BD$. Add a point $E$ on $CD$ such that $EX \perp BD$.
   

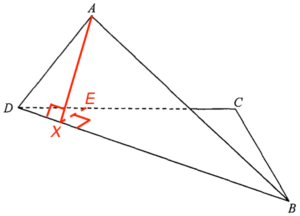
   Note that the required angle is $\angle AXE$.

   Consider $\Delta ADX$.

   $\begin{array}{rcl}
   \sin \angle ADX & = & \dfrac{AX}{AD} \\
   AX & = & 31.925\ 333\ 17 \times \sin 40^\circ \\
   AX & = & 20.521\ 208\ 6\text{ cm}
   \end{array}$

   Also,

   $\begin{array}{rcl}
   \tan \angle ADX & = & \dfrac{AX}{DX} \\
   DX & = & \dfrac{20.521\ 208\ 6}{\tan 40^\circ} \\
   DX & = & 24.456\ 224\ 07\text{ cm}
   \end{array}$

   Consider $\Delta DEX$.

   $\begin{array}{rcl}
   \tan \angle XDE & = & \dfrac{EX}{DX} \\
   EX & = & 24.456\ 224\ 07 \times \tan 20^\circ \\
   EX & = & 8.901\ 337\ 605\text{ cm}
   \end{array}$

   Also,

   $\begin{array}{rcl}
   \cos \angle EDX & = & \dfrac{DX}{DE} \\
   DE & = & \dfrac{24.456\ 224\ 07}{\cos 20^\circ} \\
   DE & = & 26.025\ 770\ 06\text{ cm}
   \end{array}$

   Consider $\Delta ADE$. Note that $\angle ADE = \angle ABC$.

   $\begin{array}{rcl}
   AE^2 & = & AD^2 + DE^2 – 2 \times AD \times DE \times \cos \angle ADE \\
   AE^2 & = & 31.925\ 333\ 17^2 + 26.025\ 770\ 06^2 – 2 \times 31.925\ 333\ 17 \times 26.025\ 770\ 06 \times \cos 37.992\ 975\ 34^\circ \\
   AE & = & 19.670\ 769\ 9\text{ cm}
   \end{array}$

   Consider $\Delta AXE$.

   $\begin{array}{rcl}
   \cos \angle AXE & = & \dfrac{AX^2 + XE^2 – AE^2}{2\times AX \times XE} \\
   \cos \angle AXE & = & \dfrac{20.521\ 208\ 6^2 + 8.901\ 337\ 605^2 – 19.670\ 769\ 9^2}{2 \times 20.521\ 208\ 6 \times 8.901\ 337\ 605} \\
   \angle AXE & = & 71.914\ 113\ 96^\circ
   \end{array}$

   Therefore, the required angle is $71.9^\circ$.