2018-I-18

$\begin{array}{rcl}
k_1 (2)^2 + k_2(2) & = & 60 \\
2k_1 + k_2 & = & 30 \ \ldots \unicode{x2460}
\end{array}$

For $f(3) = 99$, we have

$\begin{array}{rcl}
k_1(3)^2 + k_2(3) & = & 99 \\
3k_1 + k_2 & = & 33 \ \ldots \unicode{x2461}
\end{array}$

$\unicode{x2461} – \unicode{x2460}$, we have

$\begin{array}{rcl}
k_1 & = & 3
\end{array}$

Sub. $k_1 = 3$ into $\unicode{x2460}$, we have

$\begin{array}{rcl}
2(3) + k_2 & = & 30 \\
k_2 & = & 24
\end{array}$

Therefore, $f(x) = 3x^2 + 24x$.

1. By the result of (a), we have$\begin{array}{rcl}
   f(x) & = & 3x^2 + 24x \\
   & = & 3(x^2 + 8x) \\
   & = & 3\left[x^2 + 8x + \left(\dfrac{8}{2}\right)^2 – \left(\dfrac{8}{2}\right)^2\right] \\
   & = & 3(x + 4)^2 – 48
   \end{array}$

   Therefore, the coordinates of $Q$ are $(-4, -48)$.

2. Note that $y= 27 – f(x)$ means $f(x)$ is reflected about $x$ axis and then translated upwards by $27$ units. Then the $x$ coordinate of $Q$ and $R$ are the same, the $y$ coordinate of $R$$\begin{array}{cl}
   = & 27 – \text{the $y$ coordinate of $Q$} \\
   = & 27 – (-48) \\
   = & 75
   \end{array}$

   Therefore, the coordinates of $R$ are $(-4, 75)$.

3. Sketch the graph below according to the information of the question.
   

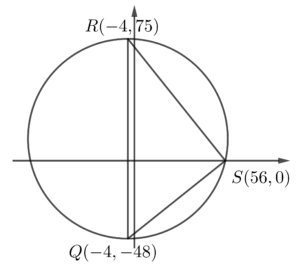
   Consider $\Delta QRS$.

   $\begin{array}{rcl}
   RS^2 + QS^2 & = & (56-(-4)^2 + (0-75)^2 + (56-(-4))^2 + (0-(-48))^2 \\
   & = & 15129
   \end{array}$

   Also,

   $\begin{array}{rcl}
   RQ^2 & = & (75-(-48))^2 \\
   & = & 15129
   \end{array}$

   Since $RS^2 + QS^2 = RQ^2$, then by the converse of the Pythagoras Theorem, $\Delta QRS$ is a right-angled triangle with $\angle QSR =90^\circ$.

   Since $\angle QSR = 90^\circ$, then by the converse of $\angle$ in the semi-circle, $QR$ is a diameter of the circle.

   Since $P$ is the circumcentre of $\Delta QRS$, then $P$ is the mid-point of $QR$.