Ans: C
Sketch the graph below according to the information provided.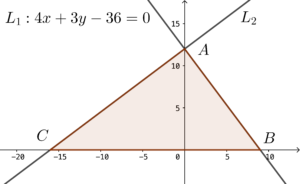
Sketch the graph below according to the information provided.

Note that $m_{L_1} = \dfrac{-4}{3}$, the $y$-intercept of $L_1 = 12$ and the $x$-intercept of $L_1 = 9$.
Since $L_2$ passes through the $y$-intercept of $L_1$ and perpendicular to $L_1$, then the equation of $L_2$ is
$\begin{array}{rcl}
\dfrac{y-12}{x-0} & = & -1 \div \dfrac{-4}{3} \\
4y – 48 & = & 3x \\
3x – 4y + 48 & = & 0
\end{array}$
Note that the $x$-intercept of $L_2 = -16$.
Hence, the required area
$\begin{array}{cl}
= & \dfrac{1}{2} \times BC \times OA \\
= & \dfrac{1}{2} \times (9 – (-16)) \times (12 – 0) \\
= & 150
\end{array}$

