I is true. If $a < 1$, the graph is like below.
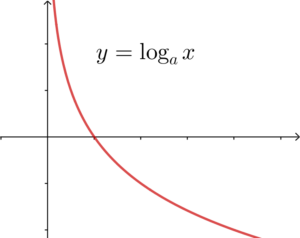
II is not true. Let $x_0$ be the $x$ coordinates of $A$ and $B$. Consider the $y$ coordinates of $A$ and $B$.
$\begin{array}{rcl}
\text{the $y$ coordinate of $A$} & > & \text{the $y$ coordinate of $B$} \\
\log_a x_0 & > & \log_b x_0 \\
\dfrac{\log x_0}{\log a} & > & \dfrac{\log x_0}{\log b} \\
\log b & > & \log a \\
b & > & a
\end{array}$
III is true. Let $x_0$ be the $x$ coordinates of $A$, $B$ and $C$. Since $ABC$ is a vertical line, then we have
$\begin{array}{rcl}
\dfrac{AB}{BC} & = & \dfrac{\text{the $y$ coordinate of $A$} – \text{the $y$ coordinate of $B$}}{\text{the $y$ coordinate of $B$}} \\
& = & \dfrac{\log_a x_0 – \log_b x_0}{\log_b x_0} \\
& = & \dfrac{\log_a x_0}{\log_b x_0} – 1 \\
& = & \dfrac{\log x_0}{\log a} \div \dfrac{\log x_0}{\log b} – 1 \\
& = & \dfrac{\log b}{\log a} – \log_a a \\
& = & \log_a b – \log_a a \\
& = & \log_a \dfrac{b}{a}
\end{array}$

