Join $AC$ and $AD$.
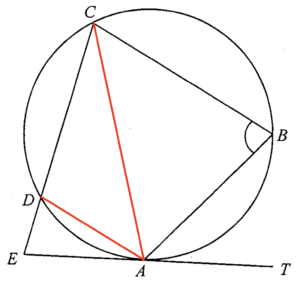
Consider $\Delta ABC$.
$\begin{array}{rcll}
\angle ACB & = & \angle BAT & \text{($\angle$s in alt. segment)} \\
\angle ACB & = & 24^\circ
\end{array}$
Also,
$\begin{array}{rcll}
\angle CAE & = & \angle ABC & \text{($\angle$s in alt. segment)}
\end{array}$
Since $AB = CD \text{(given)}$,
$\begin{array}{rcll}
\therefore \overparen{AB} & = & \overparen{CD} & \text{(eq. chords, eq. arcs)} \\
\therefore \angle CAD & = & \angle ACB & \text{(arcs and $\angle$s at $\unicode{x2299}^{ce}$ in proportion)} \\
\angle CAD & = & 24^\circ
\end{array}$
Consider $\Delta ADE$.
$\begin{array}{rcll}
\angle ADE & = & \angle ABC & \text{(ext. $\angle$, cyclic quad.)} \\
\angle DAE & = & \angle CAE – \angle CAD \\
\angle DAE & = & \angle ABC – 24^\circ
\end{array}$
Hence, we have
$\begin{array}{rcll}
\angle AED + \angle ADE + \angle DAE & = & 180^\circ & \text{($\angle$ sum of $\Delta$)} \\
72^\circ +\angle ABC + \angle ABC – 24^\circ & = & 180^\circ \\
\angle ABC & = & 66^\circ
\end{array}$

