Ans: D
On $AF$, add a point $Y$ such that $XY \perp AF$. Join $BD$ and $BY$.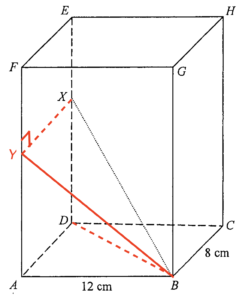
On $AF$, add a point $Y$ such that $XY \perp AF$. Join $BD$ and $BY$.

By applying Pythagoras Theorem to $\Delta ABD$, we have
$\begin{array}{rcl}
BD^2 & = & AB^2 + AD^2 \\
BD^2 & = & 12^2 + 8^2 \\
BD & = & \sqrt{208} \text{ cm}
\end{array}$
By applying Pythagoras Theorem to $\Delta BDX$, we have
$\begin{array}{rcl}
BX^2 & = & BD^2 + DX^2 \\
BX^2 & = & (\sqrt{208})^2 + 9^2 \\
BX & = & 17\text{ cm}
\end{array}$
By applying Pythagoras Theorem to $\Delta ABY$, we have
$\begin{array}{rcl}
BY^2 & = & AB^2 + AY^2 \\
BY^2 & = & 12^2 + 9^2 \\
BY & = & 15 \text{ cm}
\end{array}$
Consider $\Delta BXY$, we have
$\begin{array}{rcl}
\cos \angle XBY & = & \dfrac{BY}{BX} \\
\cos \theta & = & \dfrac{15}{17}
\end{array}$

