2019-I-17

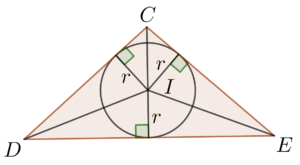
Note that the perimeter $p = CD + DE + CE$.

Note also that $CD$, $DE$ and $CE$ are tangents to the circle. Therefore, by the theorem of radius $\perp$ tangent, $r$ is the height of $\Delta CDI$, $\Delta DEI$ and $\Delta CEI$. Hence, we have

$\begin{array}{rcl}
a & = & \dfrac{1}{2} \times CD \times r + \dfrac{1}{2} \times DE \times r + \dfrac{1}{2} \times CD \times r \\
2a & = & r(CD + DE + CE) \\
2a &= & pr \\
pr & = & 2a
\end{array}$

1. Since $P$ is equidistant to $OH$ and $HK$, then $\Gamma$ is the angle bisector of $\angle OHK$.
2. Let $I(h,k)$ be the in-centre of $\Delta OHK$.
   

   $\begin{array}{rcl}
   OH & = & \sqrt{9^2 + 12^2} \\
   & = & 15 \\
   HK & = & \sqrt{(9-14)^2 + ( 12 -0)^2} \\
   & = & 13 \\
   OK & = & 14 – 0 \\
   OK & = & 14
   \end{array}$

   The area of $\Delta OHK$

   $\begin{array}{cl}
   = & \dfrac{1}{2} \times OK \times y\text{ coordinates of $H$} \\
   = & \dfrac{1}{2} \times 14 \times 12 \\
   = & 84
   \end{array}$

   Since $OK$ is a tangent to the inscribed circle of $\Delta OHK$, then the $y$ coordinate of $I$ is the radius of the circle. Then by the result of (a), we have

   $\begin{array}{rcl}
   (OH + OK + HK) \times k & = & 2 \times \text{the area of $\Delta OHK$} \\
   k & = & \dfrac{2 \times 84}{13 + 14 + 15} \\
   k & = & 4
   \end{array}$

   Consider the $\angle HOK$.

   $\begin{array}{rcl}
   \tan \angle HOK & = & \dfrac{12 – 0}{9 – 0} \\
   \angle HOK & = & \tan^{-1} \dfrac{4}{3}
   \end{array}$

   Consider the $\angle IOK$.

   $\begin{array}{rcl}
   \angle IOK & = & \dfrac{1}{2} \times \angle HOK \\
   \tan \angle IOK & = & \tan \dfrac{1}{2} \times \angle HOK \\
   \dfrac{4 – 0}{h – 0} & = & \tan \left(\dfrac{1}{2} \times \tan^{-1} \dfrac{4}{3}\right) \\
   \dfrac{4}{h} & = & \dfrac{1}{2} \\
   h & = & 8
   \end{array}$

   Therefore, the equation of $\Gamma$ is

   $\begin{array}{rcl}
   \dfrac{y – 12}{x – 9} & = & \dfrac{4 – 12}{8 – 9} \\
   y – 12 & = & 8x – 72 \\
   8x – y – 60 & = & 0
   \end{array}$