2020-I-14

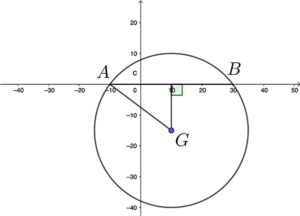
The $x$-coordinate of $G$

$\begin{array}{cl}
= & \dfrac{30 + (-10)}{2} \\
= & 10
\end{array}$

Therefore, the equation of $C$ is

$\begin{array}{rcl}
(x – 10)^2 + (y – (-15))^2 & = & (\sqrt{(30 – 10)^2 + (0 – (-15)^2})^2 \\
(x – 10)^2 + (y + 15)^2 & = & 625
\end{array}$

1. $\Gamma$ is parallel to $L$.
2. Since $\Gamma$ is parallel to $L$, then we have

   $\begin{array}{rcl}
   m_\Gamma & = & m_L \\
   m_\Gamma & = & \dfrac{0 – (-15)}{30 – 10} \\
   m_\Gamma & = & \dfrac{3}{4}
   \end{array}$

   Therefore, the equation of $\Gamma$ is

   $\begin{array}{rcl}
   \dfrac{y – 0}{x – (-10)} & = & \dfrac{3}{4} \\
   4y & = & 3(x + 10) \\
   3x – 4y + 30 & = & 0
   \end{array}$

3. 

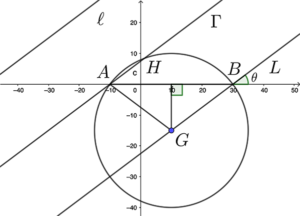
   Note that $\angle GAH = \angle GAB + \angle BAH$. Consider $\angle BAH$.

   $\begin{array}{rcl}
   \tan \angle BAH & = & m_\Gamma \\
   \tan \angle BAH & = & \dfrac{3}{4} \\
   \angle BAH & = & 36.869\ 897\ 65^\circ
   \end{array}$

   Consider $\angle BAG$. In $\Delta GAB$,

   $\begin{array}{rcll}
   GA & = & GB & \text{(radii)} \\
   \angle BAG & = & \angle ABG & \text{(base $\angle$s, isos. $\Delta$)} \\
   \angle ABG & = & \theta & \text{(vert. opp. $\angle$s)} \\
   \therefore \angle BAG & = & \theta
   \end{array}$

   Also,

   $\begin{array}{rcl}
   \tan \theta & = & m_L \\
   \tan \angle BAG & = & \dfrac{3}{4} \\
   \angle BAG & = & 36.869\ 897\ 65^\circ
   \end{array}$

   Hence, we have

   $\begin{array}{rcl}
   \angle GAH & = & \angle GAB + \angle BAH \\
   & = & 36.869\ 897\ 65^\circ + 36.869\ 897\ 65^\circ \\
   & = & 73.739\ 795\ 29^\circ \\
   & > & 70^\circ
   \end{array}$

   Therefore, I don’t agree with the claim.