Add a point $U$ on $QR$ such that $TU \perp QR$.
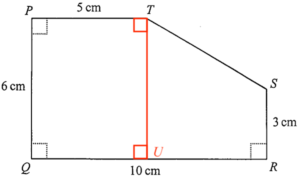
Note that $PQUT$ is a rectangle. Then $PT = QU$.
Note that the maximum absolute error
$\begin{array}{cl}
= & \dfrac{1}{2} \times 1 \\
= & 0.5 \text{ cm}
\end{array}$
For the lower bound of the area $A$, take $PT = 4.5\text{ cm}$, $PQ = 5.5\text{ cm}$, $QR = 9.5 \text{ cm}$ and $RS = 2.5 \text{ cm}$. Hence, the lower bound of the area $A$
$\begin{array}{cl}
= & 4.5 \times 5.5 + \dfrac{1}{2} \times (2.5 + 5.5) \times (9.5 – 4.5) \\
= & 44.75\text{ cm}^2
\end{array}$
For the upper bound of the area $A$, take $PT = 5.5\text{ cm}$, $PQ = 6.5\text{ cm}$, $QR = 10.5 \text{ cm}$ and $RS = 3.5 \text{ cm}$. Hence, the upper bound of the area $A$
$\begin{array}{cl}
= & 5.5 \times 6.5 + \dfrac{1}{2} \times (3.5 + 6.5) \times (10.5 – 5.5) \\
= & 60.75\text{ cm}^2
\end{array}$
Hence, the required range is $44.75 \le A < 60.75$.

