Ans: B
Add a straight line parallel to the two parallel lines as shown.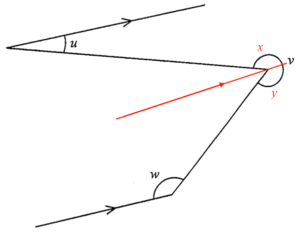
Add a straight line parallel to the two parallel lines as shown.

From the figure, we have
$\begin{array}{rcll}
w & = & y & \text{(alt. $\angle$s)} \\
u + x & = & 180^\circ & \text{(int. $\angle$s)} \\
x & = & 180^\circ – u
\end{array}$
I may not be true. If $u \neq 90^\circ$, then
$\begin{array}{cl}
& u – v + w \\
= & u – (x + y) + w \\
= & u – x – y + w \\
= & u – (180^\circ – u) – w + w \\
= & 2u – 180^\circ \\
\neq & 0 ^\circ
\end{array}$
II must be true.
$\begin{array}{cl}
& u + v – w \\
= & u + x + y – w \\
= & u + 180^\circ – u + w – w \\
= & 180^\circ
\end{array}$
III may not be true. If $w \neq 135^\circ$, then
$\begin{array}{cl}
& u + v + w \\
= & u + x + y + w \\
= & u + 180^\circ – u + w + w \\
= & 180^\circ + 2w \\
\neq & 450^\circ
\end{array}$

