2020-II-22

Ans: C
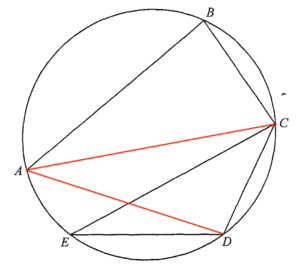
Join $AC$ and $AD$.

Consider $\Delta ABC$. Since $\angle ABC = 90^\circ$, then $AC$ is a diameter of the circle.

By applying Pythagoras Theorem to $\Delta ABC$, we have

$\begin{array}{rcl}
AC^2 & = & 10^2 + 5^2 \\
AC^2 & = & 125 \\
AC & = & \sqrt{125}\text{ cm}
\end{array}$

Consider $\Delta ACD$.

$\begin{array}{rcll}
\angle ADC & = & 90^\circ & \text{($\angle$ in semi-circle)} \\
\angle CAD & = & \angle CED & \text{($\angle$s in the same segment)} \\
\angle CAD & = & 40^\circ
\end{array}$

Hence, we have

$\begin{array}{rcl}
\sin \angle CAD & = & \dfrac{CD}{AC} \\
\sin 40^\circ & = & \dfrac{CD}{\sqrt{125}} \\
CD & = & \sqrt{125} \times \sin 40^\circ \\
CD & = & 7.186\ 583\ 952 \\
CD & \approx & 7 \text{ cm}
\end{array}$