Sketch the system of inequalities as follow.
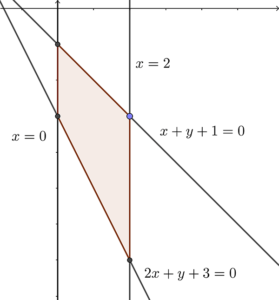
Sub. $x=0$ into $x+y+1=0$, we have
$\begin{array}{rcl}
0 + y + 1 & = & 0 \\
y & = & -1
\end{array}$
Therefore, the intersection point is $(0,-1)$.
Sub. $x=2$ into $x+y+1=0$, we have
$\begin{array}{rcl}
2 + y + 1 & = & 0 \\
y & = & -3
\end{array}$
Therefore, the intersection point is $(2,-3)$.
Sub. $x=0$ into $2x+y+3=0$, we have
$\begin{array}{rcl}
2(0) + y + 3 & = & 0 \\
y & = & -3
\end{array}$
Therefore, the intersection point is $(0,-3)$.
Sub. $x=2$ into $2x+y+3=0$, we have
$\begin{array}{rcl}
2(2) + y + 3 & = & 0 \\
y & = & -7
\end{array}$
Therefore, the intersection point is $(2,-7)$.
At $(0,-1)$,
$\begin{array}{cl}
& 4(0) + 3(-1) +k \\
= & k-3
\end{array}$
At $(2,-3)$,
$\begin{array}{cl}
& 4(2) + 3(-3) +k \\
= & k-1
\end{array}$
At $(0,-3)$,
$\begin{array}{cl}
& 4(0) + 3(-3) +k \\
= & k-9
\end{array}$
At $(2,-7)$,
$\begin{array}{cl}
& 4(2) + 3(-7) +k \\
= & k-13
\end{array}$
Obviously, the least value of $4x + 3y + k$ is $k-13$. Therefore, we have
$\begin{array}{rcl}
k – 13 & = & 24 \\
k & = & 37
\end{array}$

