Sketch a graph according to the question.
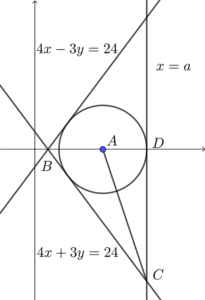
Note that $4x+3y=24$ is the reflection image of $4x-3y=24$ with respect to $x$-axis. Therefore, the triangle is an isosceles triangle with the $x$-axis as the axis of symmetry. Therefore, the in-centre lies on the $x$-axis.
Let $A$ be the in-centre. Then the coordinates of $A$ are $(31,0)$.
Sub. $y=0$ into $4x-3y=24$, we have
$\begin{array}{rcl}
4x – 3(0) & = & 24 \\
y & = & 6
\end{array}$
Note that the coordinates of $B$ are $(6,0)$.
Sub. $x=a$ into $4x+3y=24$, we have
$\begin{array}{rcl}
4a + 3y & = & 24 \\
y & = & \dfrac{24-4a}{3}
\end{array}$
Therefore, the coordinates of $C$ are $(a, \dfrac{24-4a}{3})$.
Note that the coordinates of $D$ are $(a,0)$.
Consider $\Delta BCD$.
$\begin{array}{rcl}
\tan \angle BCD & = & \dfrac{BD}{CD} \\
\tan \angle BCD & = & \dfrac{a-6}{0-\frac{24-4a}{3}} \\
\tan \angle BCD & = & \dfrac{3(a-6)}{4(a-6)} \\
\tan \angle BCD & = & \dfrac{3}{4} \\
\angle BCD & = & 36.869\ 897\ 65^\circ
\end{array}$
Consider $\Delta ACD$.
$\begin{array}{rcl}
\tan \angle ACD & = & \dfrac{AD}{CD} \\
\tan \dfrac{36.869\ 897\ 65^\circ}{2} & = & \dfrac{a-31}{0-\frac{24-4a}{3}} \\
\dfrac{1}{3} & = & \dfrac{3(a-31)}{4a-24} \\
4a – 24 & = & 9(a-31) \\
4a – 24 & = & 9a – 279 \\
5a & = & 255 \\
a & = & 51
\end{array}$

