2020-M2-06

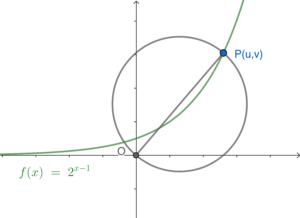
By the distance formula, we have $OP=\sqrt{u^2+v^2}$.

Let $A$ square units be the area of the circle with $OP$ as a diameter. Hence, we have

$\begin{array}{rcl}
A & = & \pi \left(\dfrac{OP}{2} \right)^2 \\
A & = & \pi \left( \dfrac{\sqrt{u^2+v^2}}{2} \right)^2 \\
A & = & \dfrac{\pi(u^2+v^2)}{4} \\
A & = & \dfrac{\pi S}{4} \\
\dfrac{dA}{dt} & = & \dfrac{\pi}{4} \times \dfrac{dS}{dt} \\
5\pi & = & \dfrac{\pi}{4} \times \dfrac{dS}{dt} \\
\dfrac{dS}{dt} & = & 20 \text{ , which is a constant.}
\end{array}$

Therefore, $S$ increases at a constant rate.

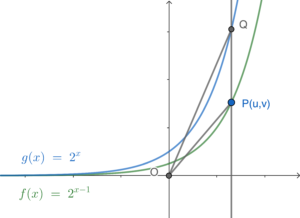
Note that the $y$-coordinate of $Q$ is $2^u$.

Let $B$ square units be the area of $\Delta OPQ$. Hence, we have

$\begin{array}{rcl}
B & = & \dfrac{1}{2} \times x\text{-coordinate of $P$} \times PQ \\
B & = & \dfrac{1}{2} \times u \times (2^u-2^{u-1}) \\
B & = & u(2^{u-1}-2^{u-2}) \\
B & = & u( 2\times 2^{u-2}-2^{u-2}) \\
B & = & u2^{u-2} \\
\dfrac{dB}{dt} & = & 2^{u-2}\times \dfrac{du}{dt} +u \times 2^{u-2} \times \ln 2 \times \dfrac{du}{dt}\\
\dfrac{dB}{dt} & = & (1+u\ln 2)2^{u-2} \dfrac{du}{dt}
\end{array}$

By the result of (a), we have

$\begin{array}{rcl}
\dfrac{dS}{dt} & = & 20 \\
\dfrac{d}{dt}(u^2+v^2) & = & 20 \\
\dfrac{d}{dt}(u^2+(2^{u-1})^2) & = & 20 \\
2u\dfrac{du}{dt}+2(2^{u-1}) \times 2^{u-1} \ln2 \times \dfrac{du}{dt} & = & 20 \\
2u\dfrac{du}{dt} +2(2^{u-1})^2\ln2\dfrac{du}{dt} & = & 20
\end{array}$

When $u=2$, we have

$\begin{array}{rcl}
2(2)\dfrac{du}{dt}+2(2^{2-1})^2\ln 2\dfrac{du}{dt} & = & 20 \\
\dfrac{du}{dt} (4-8\ln2) & = & 20 \\
\dfrac{du}{dt} & = & \dfrac{5}{1+2\ln2}
\end{array}$

Hence, when $u=2$, we have

$\begin{array}{rcl}
\dfrac{dB}{dt} & = & (1+2\ln2)2^{2-2} \times \dfrac{5}{1+2\ln2} \\
\dfrac{dB}{dt} & = & 5
\end{array}$

Therefore, the required rate of change is $5$ square units per second.