Ans: (a) $10$ (b) Yes (c) $120$
- Centre of $G$
$\begin{array}{cl}
= & \left( -\dfrac{-12}{2}, -\dfrac{-16}{2}\right) \\
= & (6, 8)
\end{array}$$\therefore OG$
$\begin{array}{cl}
= & \sqrt{(6-0)^2+(8-0)^2} \\
= & 10
\end{array}$ - Sub. $(0,0)$ into the left side of the equation of the circle $C$, we have
$\begin{array}{cl}
& 0^2 + 0^2 -12(0) -16(0) – 69 \\
= & -69 \\
< & 0 \end{array}$$\therefore O$ lies inside $C$.
- Refer to the figure. Let $F$ be the mid-point of $OG$.
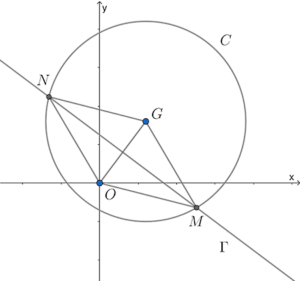
The radius of the circle
$\begin{array}{cl}
= & \sqrt{(6)^2+(8)^2 -(-69)} \\
= & 13
\end{array}$Consider $\Delta FGN$,
$\begin{array}{rcll}
NF^2 & = & NG^2 – FG^2 & \text{(Pyth. Thm.)} \\
NF^2 & = & 13^2 – (\dfrac{10}{2})^2 \\
NF^2 & = & 144 \\
NF & = & 12
\end{array}$$\therefore$ the area of quadrilateral $OMGN$
$\begin{array}{cl}
= & 2 \times \dfrac{1}{2} \times OG \times NF \\
= & 10 \times 12 \\
= & 120
\end{array}$
