2021-I-16

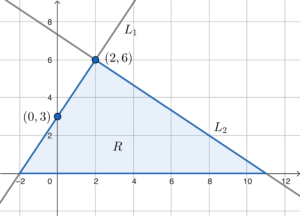
The equation of $L_1$ is

$\begin{array}{rcl}
\dfrac{y-6}{x-2} & = & \dfrac{3-6}{0-2} \\
2y-12 & = & 3x-6 \\
3x -2y +6 & = & 0
\end{array}$

Sub. $(0,0)$ into the left side of $3x -2y +6=0$, we have

$\begin{array}{cl}
& 3(0) -2(0) + 6 \\
= & 6 \\
\ge & 0
\end{array}$

Since $(0,0)$ lies in $R$, then one of the inequalities is $3x -2y +6 \ge 0$.

Since $L_1 \perp L_2$, then the slope of $L_2$

$\begin{array}{cl}
= & -1 \div m_{L_1} \\
= & -1 \div \dfrac{3}{2} \\
= & \dfrac{-2}{3}
\end{array}$

Hence, the equation of $L_2$ is

$\begin{array}{rcl}
\dfrac{y-6}{x-2} & = & \dfrac{-2}{3} \\
3y-18 & = & -2x +4 \\
2x +3y -22 & = & 0
\end{array}$

Sub. $(0,0)$ into the left side of $2x+3y-22=0$, we have

$\begin{array}{cl}
& 2(0) +3(0) -22 \\
= & -22 \\
\le & 0
\end{array}$

Since $(0,0)$ lies in $R$, then one of the inequalities is $2x +3y -22 \le 0$.

Since $R$ is above the $x$-axis, then one of the inequalities is $y\ge 0$.

Hence, the system of the inequalities is $\left\{ \begin{array}{l} 3x -2y +6 \ge 0 \\ 2x +3y -22 \le 0 \\ y \ge 0 \end{array} \right.$.

At the vertex $(-2,0)$,

$\begin{array}{cl}
& 8(-2) -5(0) \\
= & -16
\end{array}$

At the vertex $(2,6)$,

$\begin{array}{cl}
& 8(2)-5(6) \\
= & -14
\end{array}$

At the vertex $(11,0)$,

$\begin{array}{cl}
& 8(11) -5(0) \\
= & 88
\end{array}$

$\therefore$ the least value of $8x-5y$ on $R$ is $-16$.