2021-I-18

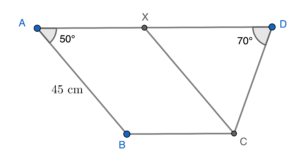
Since $AB\text{//}XC$ and $BC\text{//}AX$, then $CX=45\text{ cm}$ and $\angle CXD=50^\circ$.

In $\Delta CDX$,

$\begin{array}{rcl}
\dfrac{CD}{\sin \angle CXD} & = & \dfrac{CX}{\sin \angle CDX} \\
\dfrac{CD}{\sin 50^\circ} & = & \dfrac{45}{\sin 70^\circ} \\
CD & = & \dfrac{ 45 \sin 50^\circ}{\sin 70^\circ} \\
CD & = & 36.684\ 336\ 11\text{ cm}
\end{array}$

1. Sketch a figure according to the question.
   

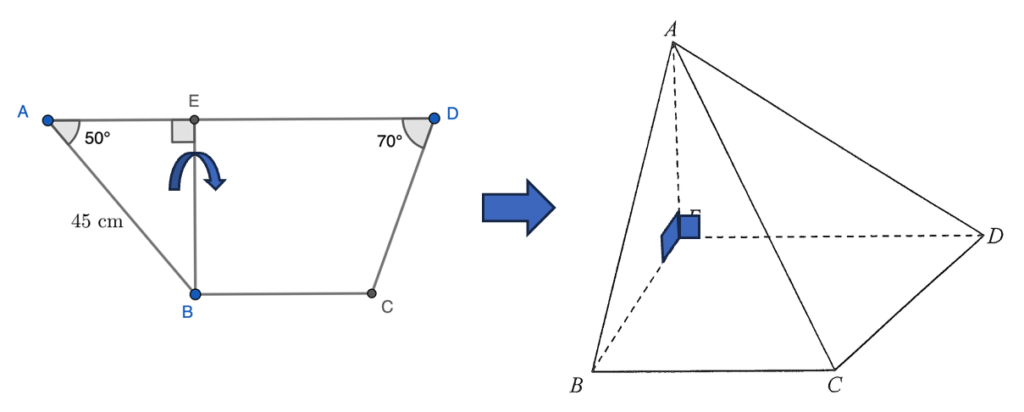
   Consider $\Delta ABE$ in trapezium $ABCD$,

   $\begin{array}{rcl}
   AE & = & AB \cos 50^\circ \\
   AE & = & 45 \cos 50^\circ \\
   AE & = & 28.925\ 442\ 44 \text{ cm}
   \end{array}$

   Consider $DE$ in trapezium $ABCD$,

   $\begin{array}{rcl}
   DE & = & BC +CD \cos 70^\circ \\
   DE & = & 40 +36.684\ 336\ 11 \cos 70^\circ \\
   DE & = & 52.546\ 781\ 89\text{ cm}
   \end{array}$

   Consider $\Delta ADE$ in the 3D figure,

   $\begin{array}{rcl}
   AD & = & \sqrt{AE^2+DE^2} \\
   AD & = & \sqrt{(28.925\ 442\ 44)^2 + (52.546\ 781\ 89)^2} \\
   AD & = & 59.982\ 043\ 21\text{ cm}
   \end{array}$

   Consider $\Delta ABC$ in the 3D figure. $\angle ABC =90^\circ$. Hence, we have

   $\begin{array}{rcl}
   AC & = & \sqrt{AB^2 +BC^2} \\
   AC & = & \sqrt{45^2 +40^2} \\
   AC & = & 60.207\ 972\ 89\text{ cm}
   \end{array}$

   Consider $\Delta ACD$ in the 3D figure,

   $\begin{array}{rcl}
   \cos \angle CAD & = & \dfrac{AC^2 +AD^2 -CD^2}{2(AC)(AD)} \\
   \cos \angle CAD & = & \dfrac{(60.207\ 972\ 89)^2 +(59.982\ 043\ 21)^2 -(36.684\ 336\ 11)^2}{2(60.207\ 972\ 89)(59.982\ 043\ 21)^2} \\
   \angle CAD & = & 35.542\ 107\ 89^\circ
   \end{array}$

2. Add a point $F$ on $CD$ such that $AD \perp CD$ and $EF\perp CD$.
   

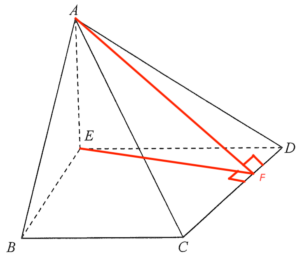
   Note that the angle between the plane $ACD$ and the plane $BCDE$ is $\angle AFE$.

   Consider $\Delta DEF$ in trapezium $ABCD$,

   $\begin{array}{rcl}
   EF & = & DE \sin \angle CDE \\
   EF & = & 52.546\ 781\ 89 \sin 70^\circ \\
   EF & = & 49.377\ 823\ 19\text{ cm}
   \end{array}$

   Consider $\Delta AEF$ in the 3D figure,

   $\begin{array}{rcl}
   \tan \angle AFE & = & \dfrac{AE}{EF} \\
   \tan \angle AFE & = & \dfrac{ 28.925\ 442\ 44}{49.377\ 823\ 19} \\
   \angle AFE & = & 30.361\ 697\ 31^\circ \\
   \angle AFE & > & 30^\circ
   \end{array}$

   $\therefore$ the angle between the plane $ACD$ and the plane $BCDE$ exceeds $30^\circ$.