2021-I-19

$\therefore$ the coordinates of $Q$ are $(6k +7, 5k +4)$.

Hence, the coordinates of the vertex will first translated to $(6k +7 -14, 5k +4) = (6k -7, 5k +4)$, and then reflect to $(-(6k-7), 5k+4) = (7-6k, 5k+4)$. Therefore, the coordinates of $R$ are $(7 -6k, 5k +4)$.

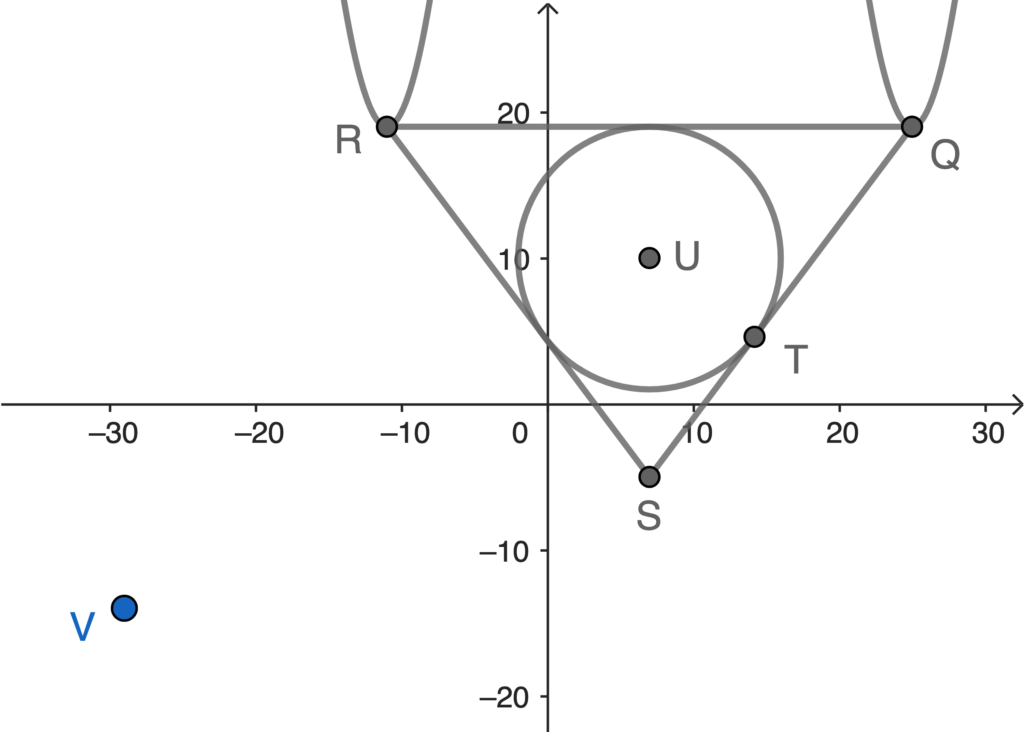
1. The equation of the straight line passes through $Q$ and $S$ is

   $\begin{array}{rcl}
   \dfrac{y-(4-3k)}{x-7} & = & \dfrac{5k +4 -(4-3k)}{6k +7 -7} \\
   \dfrac{y +3k -4}{x -7} & = & \dfrac{4}{3} \\
   3y +9k -12 & = & 4x -28 \\
   4x -3y -9k -16 & = & 0
   \end{array}$

2. Note that the $y$-coordinates of $Q$ and $R$ are the same. Therefore $QR$ is a horizontal line.

   Consider the $x$-coordinates of $Q$, $R$ and $S$.

   $\begin{array}{rcl}
   \dfrac{1}{2} (\text{$x$-coordinate of $Q$} +\text{$x$-coordinate of $R$}) & = & \dfrac{1}{2}(6k +7 + 7 -6k) \\
   & = &7 \\
   & = & \text{$x$-coordinate of $S$}
   \end{array}$

   Therefore, $\Delta QRS$ is an isosceles triangle with $SQ = SR$.

   Let $r$ be the radius of the inscribed circle $C$ of $\Delta QRS$. Then the centre of $C$ is $(7, 5k +4 -r)$.

   Hence, the equation of $C$ is $(x -7)^2 +(y -5k -4 +r)^2 = r^2$.

   $\left\{ \begin{array}{l}
   (x -7)^2 +(y -5k -4 +r)^2 = r^2 & \ldots \unicode{x2460} \\
   4x -3y -9k -16 = 0 & \ldots \unicode{x2461}
   \end{array}\right.$

   From $\unicode{x2461}$, we have

   $\begin{array}{rcl}
   4x -3y -9k -16 & = & 0 \\
   y & = & \dfrac{4x -16 -9k}{3} \ldots \unicode{x2462}
   \end{array}$

   Sub. $\unicode{x2462}$ into $\unicode{x2460}$, we have

   $\begin{array}{rcl}
   (x -7)^2 + \left(\dfrac{4x -16 -9k}{3} -5k -4 +r \right)^2 & = & r^2 \\
   x^2 -14x +49 +\dfrac{1}{9}(4x -16 -9k -15k -12 +3r)^2 -r^2 & = & 0 \\
   9x^2 -126x +441 +(4x -28 -24k +3r)^2 -9r^2 & = & 0 \\
   9x^2 -126x +441 +16x^2 +784 +576k^2 +9r^2 -224x \ \ \ \ \ & & \\
   -192kx +24rx +1344k -168r -144kr -9r^2 & = & 0 \\
   25x^2 +(24r-192k-350)x +(576k^2 -144kr +1344k -168r +1225) & = & 0 \\
   \end{array}$

   Since $QS$ is the tangent to $C$ at $T$, then we have

   $\begin{array}{rcl}
   \Delta & = & 0 \\
   (24r -192k -350)^2 -4(25)(576k^2 -144kr +1344k -168r +1225) & = & 0 \\
   576r^2 +36864k^2+ 122500 -9216kr -16800r +134400k \ \ \ \ \ & & \\
   -57600k^2 +14400kr -134400k +16800r -122500 & = & 0\\
   576r^2 -5184kr +36864k^2 & = & 0 \\
   r^2 +9kr -36k^2 & = & 0 \\
   (r-3k)(r+12k) & = & 0
   \end{array}$

   $\therefore r=3k$ or $r=-12k$ (rejected).

   Hence, the equation of $C$ is

   $\begin{array}{rcl}
   (x -7)^2 +(y-5k-4+3k)^2 & = & (3k)^2 \\
   (x-7)^2 +(y -2k -4)^2 & = & 9k^2
   \end{array}$

3. For $ST\text{//}VU$,

   $\begin{array}{rcl}
   m_{ST} & = & m_{VU} \\
   m_{QS} & = & m_{VU} \\
   \dfrac{4}{3} & = & \dfrac{-14 -(2k+4)}{-29 -7} \\
   -144 & = & -54 -6k\\
   k & = & 15
   \end{array}$

   Therefore, $ST\text{//}VU$ when $k=15$.

   For $k=15$, the graph becomes

   

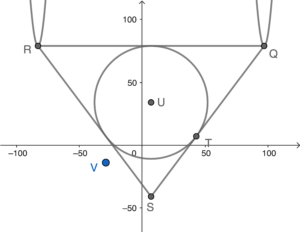
   Also, the coordinates of $S$ and $U$ are $(7,-41)$ and $(7,34)$ respectively.

   The slope of $SV$

   $\begin{array}{cl}
   = & \dfrac{-14+41}{-29 -7} \\
   = & \dfrac{-3}{4}
   \end{array}$

   Since $m_{SV} \times m_{TS}=-1$, then $SV\perp TS$.

   Since $ST$ is the tangent to $C$ at $T$ and $UT$ is a radius, then $UT \perp ST$.

   Since $SV\perp TS$ and $UT \perp ST$, then $SV\text{//}TU$.

   Hence for $k=15$, $ST\text{//}VU$ and $SV\text{//}TU$. Therefore $STUV$ is a parallelogram.

   Since $STUV$ is a parallelogram and $UT\perp ST$ (i.e. $\angle UTS =90^\circ$), then $STUV$ is a rectangle.

   Thus, it is possible that $STUV$ is a rectangle.