Ans: C
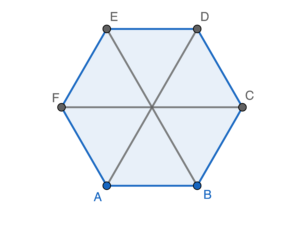

Note that the regular $6$-sided polygon can be divided into $6$ equilateral triangles with side $8\text{ cm}$.
The base area
$\begin{array}{cl}
= & 6 \times \dfrac{1}{2} \times 8 \times 8 \times \sin 60^\circ \\
= & 96\sqrt{3} \text{ cm}^2
\end{array}$
Therefore, the height of the prism
$\begin{array}{cl}
= & 288 \div 96\sqrt{3} \\
= & \dfrac{3}{\sqrt{3}} \text{ cm}
\end{array}$
Hence, the total surface area
$\begin{array}{cl}
= & 2 \times 96\sqrt{3} + 6 \times 8 \times \dfrac{3}{\sqrt{3}} \\
= & 415.692\ 193\ 8\text{ cm}^2 \\
\approx & 416\text{ cm}^2
\end{array}$

