I is true.
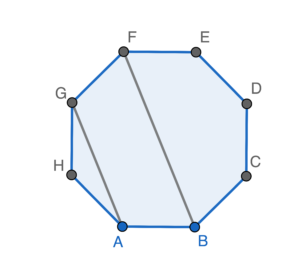
$\begin{array}{rcl}
\angle ABC & = & \dfrac{1}{8}[(8-2) \times 180^\circ ] \\
\angle ABC & = & 135^\circ \\
\angle ABF & = & \dfrac{1}{2} \times \angle ABC \\
\angle ABF & = & 67.5^\circ
\end{array}$
In $\Delta AHG$, since $AH = GH$, $\angle AGH =\angle GAH$ (base $\angle$s, isos. $\Delta$).
$\begin{array}{rcll}
\angle GAH & = & \dfrac{1}{2} (180^\circ -\angle AHG) & \text{($\angle$ sum of $\Delta$)} \\
\angle GAH & = & \dfrac{1}{2} (180^\circ -135^\circ) \\
\angle GAH & = & 22.5^\circ
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\angle BAG & = & \angle BAH -\angle GAH \\
\angle BAG & = & 135^\circ -22.5^\circ \\
\angle BAD & = & 112.5^\circ
\end{array}$
Hence, we have
$\begin{array}{cl}
& \angle ABF + \angle BAG \\
= & 67.5^\circ +112.5^\circ \\
= & 180^\circ
\end{array}$
Therefore, $AG\text{//}BF$ (int. $\angle$s supp.).
II is true.
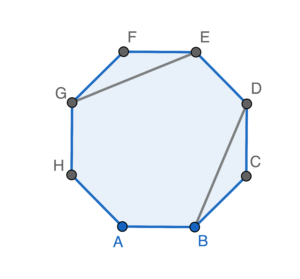
In $\Delta BCD$ and $\Delta EFG$,
$\begin{array}{rcl}
BC & = & EF & \text{(definition of regular polygon)} \\
CD & = & FG & \text{(definition of regular polygon)} \\
\angle BCD & = & \angle EFG & \text{(definition of regular polygon)} \\
\end{array}$
$\therefore \Delta BCD \cong \Delta EFG$ (S.A.S.).
Hence, $BD = EG$ (corr. sides, $\cong \Delta$).
III is true.
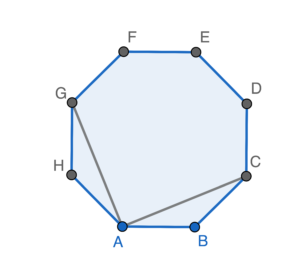
$\begin{array}{rcl}
\angle CAG & = & \angle BAH -\angle BAC -\angle GAH \\
\angle CAG & = & 135^\circ -22.5^\circ -22.5^\circ \\
\angle CAG & = & 90^circ
\end{array}$
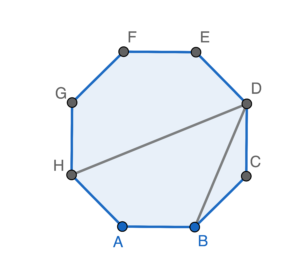
$\begin{array}{rcl}
\angle BDH & = & \dfrac{1}{2} \times \angle CDE -\angle BDC \\
\angle BDH & = & \dfrac{1}{2} \times 135^\circ -22.5^\circ \\
\angle BDH & = & 45^\circ
\end{array}$
Hence, $\angle CAG =2\angle BDH$.

