Ans: C
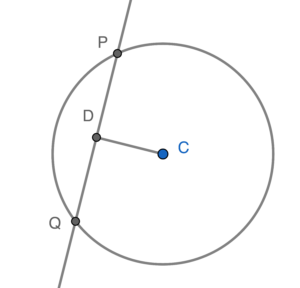

Let $C$ be the centre of the circle. Then the coordinates of $C$
$\begin{array}{cl}
= & \left( -\dfrac{-18}{2}, -\dfrac{-20}{2} \right) \\
= & (9, 10)
\end{array}$
Denote $D(s,t)$ the mid-point of $PQ$. Since $D$ is the mid-point of $PQ$, then $CD \perp PQ$ (line joining centre to mid-point of chord $\perp$ chord). Hence, we have
$\begin{array}{rcl}
m_{CD} \times m_{PQ} & = & -1 \\
\dfrac{t-10}{s-9} \times 4 & = & -1 \\
4t-40 & = & -s+9 \\
s+4t-49 & = & 0
\end{array}$

