Join $AD$.
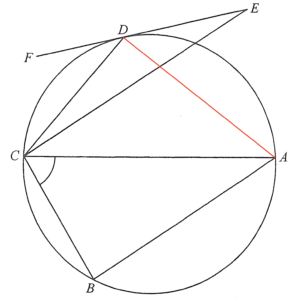
In $\Delta CDE$,
$\begin{array}{rcll}
\angle DCE & = & \angle CDF -\angle CED & \text{(ext. $\angle$ of $\Delta$)} \\
\angle DCE & = & 49^\circ -31^\circ \\
\angle DCE & = & 18^\circ
\end{array}$
In $\Delta ACD$,
$\begin{array}{rcll}
\angle ADC & = & 90^\circ & \text{($\angle$ in semi-circle)} \\
\angle CAD & = & \angle CDF & \text{($\angle$ in alt. segment)} \\
\angle CAD & = & 49^\circ \\
\angle ACE & = & 180^\circ -\angle ADC -\angle CAD -\angle DCE & \text{($\angle$ sum of $\Delta$)} \\
\angle ACE & = & 180^\circ -90^\circ -49^\circ -18^\circ \\
\angle ACE & = & 23^\circ
\end{array}$
In $\Delta ABC$,
$\begin{array}{rcll}
\angle BAC & = & \angle ACE & \text{(alt. $\angle$s, $AB$//$EC$)} \\
\angle BAC & = & 23^\circ \\
\angle ABC & = & 90^\circ & \text{($\angle$ in semi-circle)} \\
\angle ACB & = & 180^\circ -\angle ABC -\angle BAC & \text{($\angle$ sum of $\Delta$)} \\
\angle ACB & = & 180^\circ -90^\circ -23^\circ \\
\angle ACB & = & 57^\circ
\end{array}$

