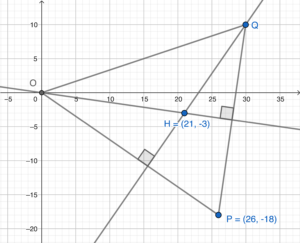
Let $Q=(x,y)$. Denote the orthocentre by $H$. Since $H$ is the orthocentre of $\Delta OPQ$, then we have $OH\perp PQ$ and $QH\perp OP$.
$\begin{array}{rcl}
OH & \perp & PQ \\
m_{OH} \times m_{PQ} & = & -1 \\
\dfrac{-3-0}{21-0} \times \dfrac{y-(-18)}{x-26} & = & -1\\
-3y-54 & = & -21x +546 \\
y & = & 7x -200 \ldots \unicode{x2460}
\end{array}$
Also,
$\begin{array}{rcl}
QH & \perp & OP \\
m_{QH} \times m_{OP} & = & -1 \\
\dfrac{y-(-3)}{x-21} \times \dfrac{-18-0}{26-0} & = & -1 \\
-18y -54 & = & -26x +546 \\
13x -9y -300 & = & 0 \ldots \unicode{x2461}
\end{array}$
Sub. $\unicode{x2460}$ into $\unicode{x2461}$, we have
$\begin{array}{rcl}
13x -9(7x-200) -300 & = & 0 \\
-50x +1500 & = & 0 \\
x & = & 30
\end{array}$
Sub. $x=30$ into $\unicode{x2460}$, we have
$\begin{array}{rcl}
y & = & 7(30) – 200 \\
y & = & 10
\end{array}$

