Sketch a graph according to the question.
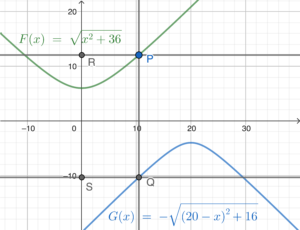
- Note that the coordinates of $P$ and $Q$ are $(u, \sqrt{u^2+36}$) and $(u,-\sqrt{(20-u)^2+16})$ respectively. Therefore, we have
$\begin{array}{cl}
& PQ \\
= & \sqrt{u^2+36}-(-\sqrt{(20-u)^2+16}) \\
= & \sqrt{u^2+36}+\sqrt{(20-u)^2+16}
\end{array}$Hence, we have
$\begin{array}{rcl}
PQ & = & \sqrt{u^2+36}+\sqrt{(20-u)^2+16} \\
\dfrac{d}{du}(PQ) & = & \dfrac{1}{2\sqrt{u^2+36}} \times 2u+\dfrac{1}{2\sqrt{(20-u)^2-+16}}\times 2(20-u)\times(-1) \\
\dfrac{d}{du}(PQ) & = & \dfrac{u}{\sqrt{u^2+36}}-\dfrac{20-u}{\sqrt{(20-u)^2+16}} \\
\dfrac{d}{du}(PQ) & = & \dfrac{u\sqrt{(20-u)^2+16}-(20-u)\sqrt{u^2+36}}{\sqrt{u^2+36}\sqrt{(20-u)^2+16}}
\end{array}$For the minimum value of $PQ$, we have
$\begin{array}{rcl}
\dfrac{d}{du}(PQ) & = & 0 \\
\dfrac{u\sqrt{(20-u)^2+16}-(20-u)\sqrt{u^2+36}}{\sqrt{u^2+36}\sqrt{(20-u)^2+16}} & = & 0 \\
u\sqrt{(20-u)^2+16}-(20-u)\sqrt{u^2+36} & = & 0 \\
u\sqrt{(20-u)^2+16} & = & (20-u)\sqrt{u^2+36} \\
u^2[(20-u)^2+16] & = & (20-u)^2(u^2+36) \\
u^2(20-u)^2+16u^2 & = & u^2(20-u)^2+36(20-u)^2 \\
4u^2 & = & 9(20-u)^2 \\
(2u)^2-(60-3u)^2 & = & 0 \\
(2u+60-3u)(2u-60+3u) & = & 0 \\
(60-u)(5u-60) & = & 0 \\
5(60-u)(u-12) & = & 0
\end{array}$Therefore, $u=60$ or $u=12$.
Since $0< x < 20$, then $a=12$.
-
- Let $A$ be the area of the rectangle $PQSR$.
$\begin{array}{rcl}
A & = & PQ \times PR \\
A & = & \left( \sqrt{u^2+36}+\sqrt{(20-u)^2+16} \right) \times (u-0) \\
A & = & u\left(\sqrt{u^2+36}+\sqrt{(20-u)^2+16}\right)
\end{array}$Hence, we have
$\begin{array}{rcl}
A & = & u\left(\sqrt{u^2+36}+\sqrt{(20-u)^2+16}\right) \\
\dfrac{d}{du}(A) & = & u\left(\dfrac{u}{\sqrt{u^2+36}}-\dfrac{20-u}{\sqrt{(20-u)^2+16}} \right)+\sqrt{u^2+36}+\sqrt{(20-u)^2+16}
\end{array}$When $u=12$, we have
$\begin{array}{rcl}
\left. \dfrac{d}{du}(A)\right|_{u=12} & = & 12\left(\dfrac{12}{\sqrt{12^2+36}}-\dfrac{20-12}{\sqrt{(20-12)^2+16}} \right)+\sqrt{12^2+36}+\sqrt{(20-12)^2+16} \\
\left. \dfrac{d}{du}(A)\right|_{u=12} & = & \dfrac{144}{\sqrt{180}}-\dfrac{96}{\sqrt{80}}+\sqrt{180}+\sqrt{80} \\
\left. \dfrac{d}{du}(A)\right|_{u=12} & = & \dfrac{24\sqrt{5}}{5}-\dfrac{24\sqrt{5}}{5}+6\sqrt{5}+4\sqrt{5} \\
\left. \dfrac{d}{du}(A)\right|_{u=12} & = & 10\sqrt{5}
\end{array}$Since $\dfrac{d}{du}(A) \neq 0$, then $A$ doest not attains its minimum value when $u=12$.
Hence, the claim is not agreed.
- Let $B$ be the perimeter of rectangle $PQSR$.
$\begin{array}{rcl}
B & = & 2(PQ+PR) \\
B & = & 2\left( \sqrt{u^2+36}+\sqrt{(20-u)^2+16}+u\right) \\
\dfrac{d}{dt}(B) & = & 2 \left( \dfrac{u}{\sqrt{u^2+36}}-\dfrac{20-u}{\sqrt{(20-u)^2+16}} + 1\right) \times \dfrac{du}{dt} \ \ldots \unicode{x2460}
\end{array}$Note that $OP = \sqrt{u^2+u^2+36}$. Hence, we have
$\begin{array}{rcl}
OP & = & \sqrt{2u^2+36} \\
\dfrac{d}{dt} (OP) & = & \dfrac{1}{2\sqrt{2u^2+36}}\times 4u \times \dfrac{du}{dt} \\
\dfrac{d}{dt}(OP) & = & \dfrac{2u}{\sqrt{2u^2+36}}\times \dfrac{du}{dt}
\end{array}$When $u=12$, we have
$\begin{array}{rcl}
\left. \dfrac{d}{dt}(OP)\right|_{u=12} & = & \dfrac{2(12)}{\sqrt{2(12)^2+36}} \times \left. \dfrac{du}{dt}\right|_{u=12} \\
28 & = &\dfrac{4}{3}\times \left. \dfrac{du}{dt}\right|_{u=12} \\
\left. \dfrac{du}{dt}\right|_{u=12} & = & 21
\end{array}$Sub. $\left. \dfrac{du}{dt}\right|_{u=12} = 21$ and $u=12$ into $\unicode{x2460}$, we have
$\begin{array}{rcl}
\left.\dfrac{d}{dt}(B)\right|_{u=12} & = & 2 \left( \dfrac{12}{\sqrt{12^2+36}}-\dfrac{20-12}{\sqrt{(20-12)^2+16}} + 1\right) \times 21 \\
\left.\dfrac{d}{dt}(B)\right|_{u=12} & = & 42
\end{array}$Therefore, the rate of change of the perimeter of the rectangle $PQSR$ is $42$ units per minute.
- Let $A$ be the area of the rectangle $PQSR$.

