2021-M2-12

1. Since $\av{AB}$ is parallel to $5\bv{i}-4\bv{j}-2\bv{k}$, then for some $\mu\in\mathbb{R}$, we have

   $\begin{array}{rcl}
   \av{AB} & = & \mu(5\bv{i}-4\bv{j}-2\bv{k}) \\
   \av{OB}-\av{OA} & = & 5\mu\bv{i}-4\mu\bv{j}-2\mu\bv{k} \\
   12\bv{i}-s\bv{j}-2\bv{k}-t\bv{i}-14\bv{j}-s\bv{k} & = & 5\mu\bv{i}-4\mu\bv{j}-2\mu\bv{k} \\
   (12-t)\bv{i}+(-s-14)\bv{j}+(-2-s)\bv{k} & = & 5\mu\bv{i}-4\mu\bv{j}-2\mu\bv{k} \\
   \end{array}$

   By comparing the components of both sides, we have

   $\left\{ \begin{array}{ll}
   12-t=5\mu & \ldots \unicode{x2460} \\
   -s-14=-4\mu & \ldots \unicode{x2461} \\
   -2-s=-2\mu & \ldots \unicode{x2462}
   \end{array}\right.$

   $\unicode{x2461}-2\times \unicode{x2462}$, we have

   $\begin{array}{rcl}
   -s-14-2(-2-s) & = & 0 \\
   s-10 & = & 0 \\
   s & = & 10
   \end{array}$

   Sub. $s=10$ into $\unicode{x2462}$, we have

   $\begin{array}{rcl}
   -2-10 & = & -2\mu \\
   \mu & = & 6
   \end{array}$

   Sub. $\mu=6$ into $\unicode{x2460}$, we have

   $\begin{array}{rcl}
   12-t & = & 5(6) \\
   12-t & = & 30 \\
   t & = & -18
   \end{array}$

2. The required area
   

   $\begin{array}{cl}
   = & \dfrac{1}{2} \left| \av{AB} \times \av{AC} \right| \\
   = & \dfrac{1}{2} \left| (5\mu\bv{i}-4\mu\bv{j}-2\mu\bv{k})\times(\av{OC}-\av{OA})\right| \\
   = & \dfrac{1}{2} \left| (30\bv{i}-24\bv{j}-12\bv{k})\times(12\bv{i}-16\bv{j}+10\bv{k}+18\bv{i}-14\bv{j}-10\bv{k})\right| \\
   = & \dfrac{1}{2} \left|(30\bv{i}-24\bv{j}-12\bv{k})\times(30\bv{i}-30\bv{j}) \right| \\
   = & \dfrac{1}{2} \left| \begin{vmatrix} \bv{i} & \bv{j} & \bv{k} \\ 30 & -24 & -12 \\ 30 & -30 & 0 \end{vmatrix}\right| \\
   = & \dfrac{1}{2} \left| \begin{vmatrix} -24 & -12 \\ -30 & 0 \end{vmatrix} \bv{i} -\begin{vmatrix} 30 & -12 \\ 30 & 0 \end{vmatrix} \bv{j}+\begin{vmatrix} 30 & -24 \\ 30 & -30 \end{vmatrix} \bv {k}\right| \\
   = & \dfrac{1}{2}|-360\bv{i}-360\bv{j}-180\bv{k}| \\
   = & \dfrac{1}{2} \sqrt{(-360)^2+(-360)^2+(-180)^2} \\
   = & 270
   \end{array}$

3. This is out of syllabus after 2022.

   Sketch a graph according to the question.

   

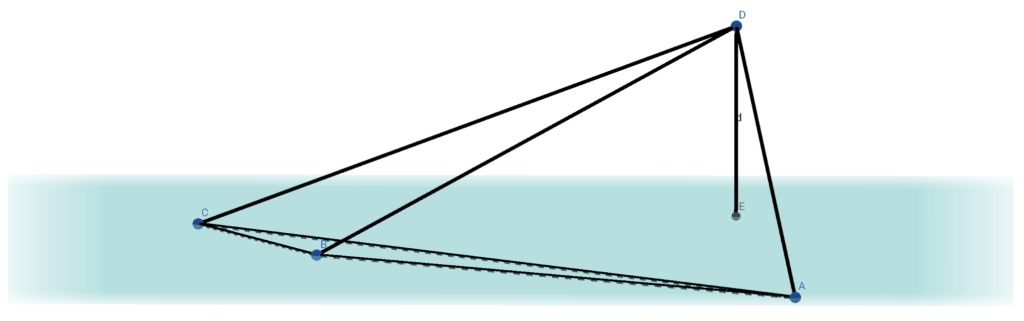
   The required volume

   $\begin{array}{cl}
   = & \dfrac{1}{6} \left|(\av{AB}\times \av{AC})\cdot\av{AD}\right| \\
   = & \dfrac{1}{6} \left| (-360\bv{i}-360\bv{j}-180\bv{j}) \cdot (\av{OD}-\av{OA})\right| \\
   = & \dfrac{1}{6} \left| (-360\bv{i}-360\bv{j}-180\bv{j}) \cdot (18\bv{i}+12\bv{j}+14\bv{k}+18\bv{i}-14\bv{j}-10\bv{k})\right| \\
   = & \dfrac{1}{6} \left| (-360\bv{i}-360\bv{j}-180\bv{j}) \cdot (36\bv{i}-2\bv{j}+4\bv{k})\right| \\
   = & \dfrac{1}{6} \left| (-360)(36)+(-360)(-2)+(-180)(4)\right| \\
   = & \dfrac{1}{6} |-12960| \\
   = & 2160
   \end{array}$

4. Let $d$ be the shortest distance from $D$ to $\Pi$.

   $\begin{array}{rcl}
   \dfrac{1}{3} \times \text{area of }\Delta ABC \times d & = & \text{volume of the tetrahedron } ABCD \\
   \dfrac{1}{3} \times 270 \times d & = & 2160 \\
   d & = & 24
   \end{array}$

   Therefore, the shortest distance from $D$ to $\Pi$ is $24$.

Consider $\av{DE}$, we have

$\begin{array}{cl}
& \av{DE} \\
= & \left(\dfrac{\av{AD}\cdot(\av{AB}\times\av{AC})}{|\av{AB}\times\av{AC}|} \right) \times \dfrac{\av{AB}\times\av{AC}}{|\av{AB}\times\av{AC}|} \\
= & d \times \dfrac{-360\bv{i}-360\bv{j}-180\bv{k}}{\sqrt{(-360)^2+(-360)^2+(-180)^2}} \\
= & 24 \times \dfrac{-360\bv{i}-360\bv{j}-180\bv{k}}{540} \\
= & -16\bv{i}-16\bv{j}-8\bv{k}
\end{array}$

Hence, we have

$\begin{array}{rcl}
\av{EA} & = & \av{DA}-\av{DE} \\
\av{EA} & = & -36\bv{i}+2\bv{j}-4\bv{k} +16\bv{i}+16\bv{j}+8\bv{k} \\
\av{EA} & = & -20\bv{i}+18\bv{j}+4\bv{k}
\end{array}$

Also, we have

$\begin{array}{rcl}
\av{EB} & = & \av{EA}+\av{AB} \\
\av{EB} & = & -20\bv{i}+18\bv{j}+4\bv{k}+30\bv{i}-24\bv{j}-12\bv{k} \\
\av{EB} & = & 10\bv{i}-6\bv{j}-8\bv{k}
\end{array}$

Consider $\Delta ABE$, by the section formula, we have

$\begin{array}{rcl}
\av{EM} & = & \dfrac{1}{2}\left(\av{EA}+\av{EB}\right) \\
\av{EM} & = & \dfrac{1}{2}(-20\bv{i}+18\bv{j}+4\bv{k}+10\bv{i}-6\bv{j}-8\bv{k}) \\
\av{EM} & = & \dfrac{1}{2}(-10\bv{i}+12\bv{j}-4\bv{k}) \\
\av{EM} & = & -5\bv{i}+6\bv{j}-2\bv{k}
\end{array}$

Hence, we have

$\begin{array}{cl}
& \av{EM}\cdot\av{AB} \\
= & (-5\bv{i}+6\bv{j}-2\bv{k})\cdot(30\bv{i}-24\bv{j}-12\bv{k}) \\
= & (-5)(30)+(6)(-24)+(-2)(-12) \\
= & -270 \\
\neq & 0
\end{array}$

Therefore, $EM$ is not perpendicular to $AB$.

Hence, $EM$ is not the perpendicular bisector of $AB$.

Hence, $E$ is not the circumcentre of $\Delta ABC$.