Ans: (a) $20$ (b) (i) $GH$ is perpendicular to $GP$. (ii) $220$
- The coordinates of $G$
$\begin{array}{cl}
= & \left( -\dfrac{-154}{2}, -\dfrac{-128}{2} \right) \\
= & (77, 64)
\end{array}$Therefore, the distance between $G$ and $H$
$\begin{array}{cl}
= & \sqrt{(77-65)^2 +(64-48)^2} \\
= & 20
\end{array}$ - Sketch the graph according to the question.
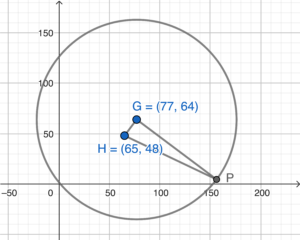
- For the area of $\Delta GHP$ is the greatest, $GP$ must be a radius and $\angle HGP =90^\circ$. Therefore $GH$ is perpendicular to $GP$.
- Note that $GP$ is a radius of $C$. Then we have
$\begin{array}{rcl}
GP & = & \sqrt{77^2+64^2-224} \\
GP & = & 99
\end{array}$In $\Delta GHP$,
$\begin{array}{rcll}
HP^2 & = & HG^2 +GP^2 & \text{(Pyth. Thm.)} \\
HP & = & \sqrt{20^2 +99^2} \\
HP & = & 101
\end{array}$Therefore, the perimeter of $\Delta GHP$
$\begin{array}{cl}
= & 20 + 99 + 101 \\
= & 220
\end{array}$

