2022-I-18

1. By using cosine law, we have

   $\begin{array}{rcl}
   QR^2 & = & PR^2 +PQ^2 -2(PR)(PQ)\cos \angle QPR \\
   QR^2 & = & 25^2 +30^2 -2(25)(30)\cos 95^\circ \\
   QR & = & 40.690\ 706\ 73\text{ cm}
   \end{array}$

2. By using sine law, we have

   $\begin{array}{rcl}
   \dfrac{PR}{\sin \angle PQR} & = & \dfrac{QR}{\sin \angle QPR} \\
   \dfrac{25}{\sin \angle PQR} & = & \dfrac{40.690\ 706\ 73}{\sin 95^\circ} \\
   \angle PQR & = & 37.738\ 093\ 75^\circ
   \end{array}$

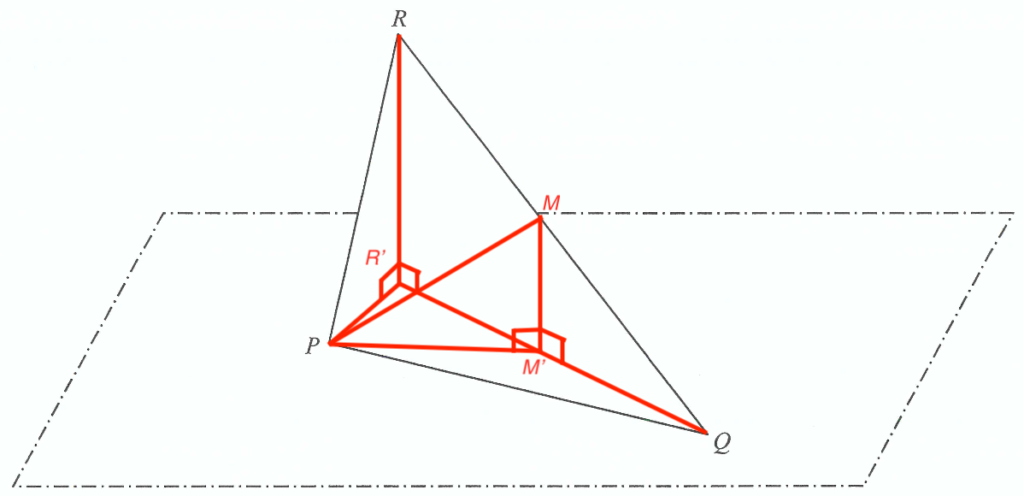
Note that the required angle is $\angle MPM’$.

In $\Delta MPQ$,

$\begin{array}{rcl}
MP^2 & = & PQ^2 +QM^2 -2(PQ)(QM)\cos \angle PQM \\
MP^2 & = & 30^2 +\left(\dfrac{40.690\ 706\ 73}{2}\right)^2 -2(30)\left(\dfrac{40.690\ 706\ 73}{2}\right) \cos 37.738\ 093\ 75^\circ \\
MP & = & 18.669\ 938\ 31\text{ cm}
\end{array}$

Since $RR’\text{//}MM’$ and $M$ is the mid-point of $QR$, we have

$\begin{array}{rcl}
MM’ & = & \dfrac{1}{2} RR’ \\
MM’ & = & \dfrac{1}{2} PR \sin \angle RPR’ \\
MM’ & = & \dfrac{1}{2} (25) \sin 70^\circ \\
MM’ & = & 11.746\ 157\ 76\text{ cm}
\end{array}$

In $\Delta MPM’$,

$\begin{array}{rcl}
\sin \angle MPM’ & = & \dfrac{MM’}{MP} \\
\sin \angle MPM’ & = & \dfrac{11.746\ 157\ 76}{18.669\ 938\ 31} \\
\angle MPM’ & = & 38.987\ 304\ 93^\circ \\
\angle MPM’ & < & 40^\circ \end{array}$

Therefore, the claim is not correct.