Join $PN$.
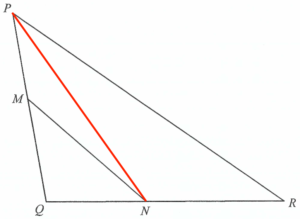
Let $x\text{ cm}^2$ be the area of $\Delta MNQ$. Since $\Delta MNP$ and $\Delta MNQ$ have the same height with respect to the bases $MP$ and $MQ$ respectively, then we have
$\begin{array}{rcl}
\dfrac{\text{area of $\Delta MNP$}}{\text{area of $\Delta MNQ$}} & = &\dfrac{PM}{MQ} \\
\dfrac{\text{area of $\Delta MNP$}}{x} & =& \dfrac{5}{6} \\
\text{area of $\Delta MNP$} & = & \dfrac{5x}{6} \text{ cm}^2
\end{array}$
Since $\Delta NPR$ and $\Delta NPQ$ have the same height with respect to the bases $NR$ and $NQ$ respectively, then we have
$\begin{array}{rcl}
\dfrac{\text{area of $\Delta PNR$}}{\text{area of $\Delta NPQ$}} & = &\dfrac{NR}{NQ} \\
\dfrac{59 -\frac{5x}{6}}{x+\frac{5x}{6}} & =& \dfrac{4}{3} \\
177-\dfrac{5x}{2} & = & 4x +\dfrac{10x}{3} \\
\dfrac{59}{6} x & = & 177 \\
x & = & 18
\end{array}$
Therefore, the area of $\Delta MNQ$ is $18\text{ cm}^2$.

