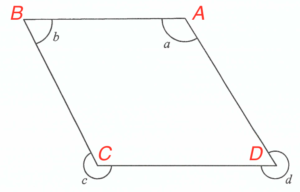
Denote the four vertices by $A$, $B$, $C$ and $D$ as shown in the figure.
I must be true. Since $AD\text{//} BC$, then $a+b=180^\circ \text{ (int. $\angle$s, $AD$//$BC$)}$.
II may not be true. Assume $b=30^\circ$. Then we have
$\begin{array}{rcll}
\angle BCD +b & = & 180^\circ & \text{(int. $\angle$s, $AB$//$DC$)} \\
\angle BCD & = & 180^\circ -b \\
\angle BCD & = & 180^\circ -30\circ \\
\angle BCD & = & 150^\circ
\end{array}$
Also,
$\begin{array}{rcll}
\angle BCD +c & = & 360^\circ & \text{($\angle$s at a point)} \\
150^\circ +c & = & 360^\circ \\
c & = & 210^\circ
\end{array}$
Therefore, $b+c \neq 360^\circ$ in this case.
III must be true. Note that $\angle ADC = b \text{ (app. $\angle$ of parallelogram)}$.
$\begin{array}{rcll}
\text{relfex} \angle BCD +\angle BCD + \text{reflex} \angle ADC +\angle ADC & = & 720^\circ \\
c +180^\circ -b +d +b & = & 720^\circ \\
b+c & = & 540^\circ
\end{array}$

